Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-26T22:16:13.928Z Has data issue: false hasContentIssue false
  • English
  • Français

On the sum of the square of a prime and a square-free number

Part of: Multiplicative number theory Additive number theory; partitions

Published online by Cambridge University Press:  01 January 2016

Adrian W. Dudek  and
David J. Platt
Adrian W. Dudek
Affiliation:
Mathematical Sciences Institute, The Australian National University, Acton ACT 2601, Australia email adrian.dudek@anu.edu.au
David J. Platt
Affiliation:
Heilbronn Institute for Mathematical Research, University of Bristol, Bristol BS8 1SN, United Kingdom email dave.platt@bris.ac.uk

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that every integer 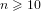$n\geqslant 10$ such that 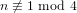$n\not \equiv 1\text{ mod }4$ can be written as the sum of the square of a prime and a square-free number. This makes explicit a theorem of Erdős that every sufficiently large integer of this type may be written in such a way. Our proof requires us to construct new explicit results for primes in arithmetic progressions. As such, we use the second author’s numerical computation regarding the generalised Riemann hypothesis to extend the explicit bounds of Ramaré–Rumely.

MSC classification

Primary: 11N13: Primes in progressions 11P32: Goldbach-type theorems; other additive questions involving primes
Type
Research Article
Information
LMS Journal of Computation and Mathematics , Volume 19 , Issue 1 , 2016 , pp. 16 - 24
Copyright
© The Author(s) 2016 

References

ACRC, University of Bristol, BlueCrystal Phase 3 User Guide, 2014,https://www.acrc.bris.ac.uk/pdf/bc-user-guide.pdf.Google Scholar
Batut, C., Belabas, K., Bernardi, D., Cohen, H. and Olivier, M., User’s Guide to PARI-GP, 2000,http://pari.math.u-bordeaux.fr/pub/pari/manuals/2.3.3/users.pdf.Google Scholar
Booker, A. R., Hiary, G. A. and Keating, J. P., ‘Detecting squarefree numbers’, Duke Math. J. 164 (2015) no. 2, 235–275.CrossRefGoogle Scholar
Davenport, H., The higher arithmetic: an introduction to the theory of numbers , 8th edn (Cambridge University Press, 2008).CrossRefGoogle Scholar
Dudek, A. W., ‘On the sum of a prime and a square-free number’, Ramanujan J. (2015), to appear.CrossRefGoogle Scholar
Dusart, P., ‘Inégalités explicites pour 𝜓(x), 𝜃(x), 𝜋(x) et les nombres premiers’, C. R. Math. Rep. Acad. Sci. Can. 21 (1999) no. 1, 53–59.Google Scholar
Erdős, P., ‘The representation of an integer as the sum of the square of a prime and of a square-free integer’, J. Lond. Math. Soc. 4 (1935) 243–245.CrossRefGoogle Scholar
Montgomery, H. L. and Vaughan, R. C., ‘The large sieve’, Mathematika 20 (1973) 119–134.CrossRefGoogle Scholar
Platt, D. J., ‘Numerical computations concerning the GRH’, Math. Comp. (2015), to appear.CrossRefGoogle Scholar
Ramaré, O. and Rumely, R., ‘Primes in arithmetic progressions’, Math. Comp. 65 (1996) no. 213, 397–425.CrossRefGoogle Scholar
Robin, G., ‘Estimation de la fonction de Tchebychef 𝜃 sur le k-ième nombre premier et grandes valeurs de la fonction 𝜔(n) nombre de diviseurs premiers de n ’, Acta Arith. 42 (1983) no. 4, 367–389.CrossRefGoogle Scholar
Rumely, R., ‘Numerical computations concerning the ERH’, Math. Comp. 61 (1993) no. 203, 415–440.CrossRefGoogle Scholar
Walisch, K., PrimeSieve, http://primesieve.org/.Google Scholar