Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-20T01:31:01.778Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-commutative Iwasawa theory for elliptic curves with multiplicative reduction

Published online by Cambridge University Press:  15 October 2015

DANIEL DELBOURGO  and
ANTONIO LEI
DANIEL DELBOURGO
Affiliation:
Department of Mathematics, University of Waikato, Hamilton 3240, New Zealand. e-mail: delbourg@waikato.ac.nz
ANTONIO LEI
Affiliation:
Département de Mathématiques et de Statistique, Université Laval, Québec QC, CanadaG1V 0A6. e-mail: antonio.lei@mat.ulaval.ca
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $E_{/{\mathbb{Q}}}$ be a semistable elliptic curve, and p ≠ 2 a prime of bad multiplicative reduction. For each Lie extension 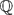$\mathbb{Q}$FT/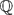$\mathbb{Q}$ with Galois group G∞ ≅ 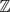$\mathbb{Z}$p ⋊ 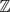$\mathbb{Z}$p×, we construct p-adic L-functions interpolating Artin twists of the Hasse–Weil L-series of the curve E. Through the use of congruences, we next prove a formula for the analytic λ-invariant over the false Tate tower, analogous to Chern–Yang Lee's results on its algebraic counterpart. If one assumes the Pontryagin dual of the Selmer group belongs to the $\mathfrak{M}_{\mathcal{H}}$(G∞)-category, the leading terms of its associated Akashi series can then be computed, allowing us to formulate a non-commutative Iwasawa Main Conjecture in the multiplicative setting.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 160 , Issue 1 , January 2016 , pp. 11 - 38
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barré-Sirieix, K., Diaz, G., Gramain, F. and Philibert, G.Une preuve de la conjecture de Mahler-Manin. Invent. Math. 124 (1996), no. 1–3, 1–9.CrossRefGoogle Scholar
[2]Bouganis, A.Special values of L-functions and false Tate curve extensions. J. London Math. Soc. 82 (2010), 596–620.CrossRefGoogle Scholar
[3]Bouganis, A. and Dokchitser, V.Algebraicity of L-values for elliptic curves in a false Tate curve tower. Math. Proc. Camb. Phil. Soc. 142 (2007), no. 2, 193–204.CrossRefGoogle Scholar
[4]Coates, J., Fukaya, T., Kato, K., Sujatha, R. and Venjakob, O.The GL2 main conjecture for elliptic curves without complex multiplication. Inst. Hautes Études Sci. Publ. Math. 101 (2005), 163–208.CrossRefGoogle Scholar
[5]Coleman, R. and McCallum, W.Stable reduction of Fermat curves and Jacobi sum Hecke characters. J. Reine Angew. Math. 385 (1988), 41–101.Google Scholar
[6]Delbourgo, D. and Lei, A. Transition formulae for ranks of abelian varieties. To appear in Rocky Mountain Math. Journal (2015).CrossRefGoogle Scholar
[7]Delbourgo, D. and Ward, T.Non-abelian congruences between L-values of elliptic curves. Ann. Inst. Fourier (Grenoble) 58 (2008), no. 3, 1023–1055.CrossRefGoogle Scholar
[8]Delbourgo, D. and Ward, T.The growth of CM periods over false Tate extensions. Experiment. Math. 19 (2010), no. 2, 195–210.CrossRefGoogle Scholar
[9]Delbourgo, D. Exceptional zeroes of p-adic L-functions over non-abelian field extensions. To appear in Glasgow Math. Journal (2015).CrossRefGoogle Scholar
[10]Delbourgo, D.On trivial p-adic zeroes for elliptic curves over Kummer extensions. New Zealand J. Math. 45 (2015), 33–38.Google Scholar
[11]Dokchitser, T. and Dokchitser, V.Computations in non-commutative Iwasawa theory. Proc. London Math. Soc. (3) 94 (2007), 211–272.CrossRefGoogle Scholar
[12]Dokchitser, V.Root numbers of non-abelian twists of elliptic curves. Proc. London Math. Soc. (3) 91 (2005), 300–324.CrossRefGoogle Scholar
[13]Greenberg, R. and Stevens, G.p-adic L-functions and p-adic periods of modular forms. Invent. Math. 111 (1993), 401–447.CrossRefGoogle Scholar
[14]Jones, J. W.Iwasawa L-functions for multiplicative abelian varieties. Duke Math. J. 59 (1989), no. 2, 399–420.CrossRefGoogle Scholar
[15]Kato, K.K 1 of some non-commutative completed group rings. K-theory 34 (2005), no. 2, 99–140.CrossRefGoogle Scholar
[16]Lee, C.-Y.Non-commutative Iwasawa theory of elliptic curves at primes of multiplicative reduction. Math. Proc. Camb. Phil. Soc. 154 (2013), no. 2, 303–324.CrossRefGoogle Scholar
[17]Mazur, B., Tate, J. and Teitelbaum, J.On p-adic analogues of the conjectures of Birch and Swinnerton-Dyer. Invent. Math. 84 (1986), no. 1, 1–48.CrossRefGoogle Scholar
[18]Panchishkin, A. A.Non-Archimedean L-functions of Siegel and Hilbert modular formsLecture Notes in Math. vol. 1471 (Springer-Verlag, 1991).Google Scholar
[19]Schneider, P.p-adic height pairings. I Invent. Math. 69 (1982), no. 3, 401–409.CrossRefGoogle Scholar
[20]Schneider, P.p-adic height pairings. II Invent. Math. 79 (1985), no. 2, 329–374.CrossRefGoogle Scholar
[21]Serre, J.-P.Sur les représentations modulaires de degré 2 de Gal($\overline{\mathbb{Q}}$/$\mathbb{Q}$). Duke Math. J. 54 (1987), no. 1, 179–230.CrossRefGoogle Scholar
[22]Sharifi, R.On norm residue symbols and conductors. J. Number Theory 86 (2001), no. 2, 196–209.CrossRefGoogle Scholar
[23]Shimura, G.Special values of the zeta functions associated with Hilbert modular forms. Duke Math. J. 45 (1978), no. 3, 637–679.CrossRefGoogle Scholar
[24]Tate, J.Number theoretic background. Proc. Symp. Pure Math. 33 (1979), (2) p 3–26.CrossRefGoogle Scholar
[25]Viviani, F.Ramification groups and Artin conductors of radical extensions of $\mathbb{Q}$. J. Théor. Nombres Bordeaux 16 (2004), no. 3, 779–816.CrossRefGoogle Scholar
[26]Zerbes, S. L.Generalised Euler characteristics of Selmer groups. Proc. Lond. Math. Soc. 98 (2009), no. 3, 775–96.CrossRefGoogle Scholar
[27]Zerbes, S. L.Akashi series of Selmer groups. Math. Proc. Camb. Phil. Soc. 151 (2011), no. 2, 229–243.CrossRefGoogle Scholar