Hostname: page-component-8448b6f56d-xtgtn Total loading time: 0 Render date: 2024-04-19T19:57:20.043Z Has data issue: false hasContentIssue false
  • English
  • Français

A Titchmarsh divisor problem for elliptic curves

Published online by Cambridge University Press:  10 November 2015

PAUL POLLACK
PAUL POLLACK*
Affiliation:
Department of Mathematics, University of Georgia, Athens, Georgia, U.S.A. e-mail: pollack@uga.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let E/Q be an elliptic curve with complex multiplication. We study the average size of τ(#E(Fp)) as p varies over primes of good ordinary reduction. We work out in detail the case of E: y2 = x3 − x, where we prove that

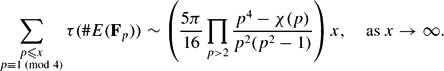$$\begin{equation} \sum_{\substack{p \leq x \\p \equiv 1\pmod{4}}} \tau(\#E({\bf{F}}_p)) \sim \left(\frac{5\pi}{16} \prod_{p > 2} \frac{p^4-\chi(p)}{p^2(p^2-1)}\right)x, \quad\text{as $x\to\infty$}. \end{equation}$$
Here χ is the nontrivial Dirichlet character modulo 4. The proof uses number field analogues of the Brun–Titchmarsh and Bombieri–Vinogradov theorems, along with a theorem of Wirsing on mean values of nonnegative multiplicative functions.

Now suppose that E/Q is a non-CM elliptic curve. We conjecture that the sum of τ(#E(Fp)), taken over p ⩽ x of good reduction, is ~cEx for some cE > 0, and we give a heuristic argument suggesting the precise value of cE. Assuming the Generalized Riemann Hypothesis for Dedekind zeta functions, we prove that this sum is ≍Ex. The proof uses combinatorial ideas of Erdős.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 160 , Issue 1 , January 2016 , pp. 167 - 189
Copyright
Copyright © Cambridge Philosophical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Akbary, A. and Felix, A. T.On invariants of elliptic curves on average. Acta Arith. 168 (2015), 31–70.CrossRefGoogle Scholar
[2]Akbary, A. and Ghioca, D.A geometric variant of Titchmarsh divisor problem. Int. J. Number Theory 8 (2012), 53–69.CrossRefGoogle Scholar
[3]Clark, P. L., Cook, B. and Stankewicz, J.Torsion points on elliptic curves with complex multiplication (with an appendix by Alex Rice). Int. J. Number Theory 9 (2013), 447–479.CrossRefGoogle Scholar
[4]Castryck, W. and Hubrechts, H.The distribution of the number of points modulo an integer on elliptic curves over finite fields. Ramanujan J. 30 (2013), 223–242.CrossRefGoogle Scholar
[5]Childress, N.Class Field Theory (Springer, New York, 2009).CrossRefGoogle Scholar
[6]Cojocaru, A. C.Reductions of an elliptic curve with almost prime orders. Acta Arith. 119 (2005), 265–289.CrossRefGoogle Scholar
[7]Duke, W.Almost all reductions modulo p of an elliptic curve have a large exponent. C. R. Math. Acad. Sci. Paris 337 (2003), 689–692.CrossRefGoogle Scholar
[8]David, C. and Wu, J.Almost prime values of the order of elliptic curves over finite fields. Forum Math. 24 (2012), 99–119.CrossRefGoogle Scholar
[9]David, C. and Wu, J.Pseudoprime reductions of elliptic curves. Canad. J. Math. 64 (2012), 81–101.CrossRefGoogle Scholar
[10]Elkies, N. D.Distribution of supersingular primes. Astérisque (Proceedings of Journées Arithmétiques, Luminy, 1989) 198–200 (1992), 127–132.Google Scholar
[11]Elliott, P. D. T. A.On the mean value of f(p). Proc. London Math. Soc. (3) 21 (1970), 28–96.CrossRefGoogle Scholar
[12]Erdős, P.On the sum ∑xk = 1d(f(k)). J. London Math. Soc. 27 (1952), 7–15.Google Scholar
[13]Friedlander, J. B. and Iwaniec, H.Divisor weighted sums. Zap. Nauchn. Sem. POMI 322 (2005), 212–219.Google Scholar
[14]Felix, A. T. and Ram Murty, M.On the asymptotics for invariants of elliptic curves modulo p. J. Ramanujan Math. Soc. 28 (2013), 271–298.Google Scholar
[15]Gekeler, E.-U.The distribution of group structures on elliptic curves over finite prime fields. Doc. Math. 11 (2006), 119–142 (electronic).CrossRefGoogle Scholar
[16]Gun, S. and Ram Murty, M.Divisors of Fourier coefficients of modular forms. New York J. Math. 20 (2014), 229–239.Google Scholar
[17]Granville, A.Smooth numbers: computational number theory and beyond. Algorithmic Number Theory: Lattices, Number Fields, Curves and Cryptography. Math. Sci. Res. Inst. Publ. 44 (Cambridge University Press, Cambridge, 2008), 267–323.Google Scholar
[18]Hinz, J. and Lodemann, M.On Siegel zeros of Hecke-Landau zeta-functions. Monatsh. Math. 118 (1994), 231–248.CrossRefGoogle Scholar
[19]Howe, E. W.On the group orders of elliptic curves over finite fields. Compositio Math. 85 (1993), 229–247.Google Scholar
[20]Halberstam, H. and Richert, H.-E.Sieve methods. London Math. Soc. Monogr. 4 (Academic Press, London-New York, 1974).Google Scholar
[21]Huxley, M. N.The large sieve inequality for algebraic number fields. III. Zero-density results. J. London Math. Soc. (2) 3 (1971), 233–240.CrossRefGoogle Scholar
[22]Hardy, G. H. and Wright, E. M.An introduction to the theory of numbers (sixth ed.) (Oxford University Press, Oxford, 2008).CrossRefGoogle Scholar
[23]Jiménez Urroz, J.Almost prime orders of CM elliptic curves modulo p. Algorithmic Number Theory. Lecture Notes in Comput. Sci. 5011 (Springer, Berlin, 2008), 74–87.CrossRefGoogle Scholar
[24]Lang, S.Elliptic Functions (second ed.). Grad. Texts in Math. 112 (Springer-Verlag, New York, 1987).CrossRefGoogle Scholar
[25]Lenstra, H. W. Jr.Factoring integers with elliptic curves. Ann. of Math. (2) 126 (1987), 649–673.CrossRefGoogle Scholar
[26]Linnik, U. V.The dispersion method in binary additive problems. Trans. math. monogr. 4 (Amer. Math. Soc., Providence, RI, 1963).Google Scholar
[27]Moree, P. and Cazaran, J.On a claim of Ramanujan in his first letter to Hardy. Expo. Math. 17 (1999), 289–311.Google Scholar
[28]Rajwade, A. R.Arithmetic on curves with complex multiplication by √ − 2. Proc. Camb. Phil. Soc. 64 (1968), 659–672.CrossRefGoogle Scholar
[29]Serre, J.-P.Propriétés galoisiennes des points d'ordre fini des courbes elliptiques. Invent. Math. 15 (1972), 259–331.CrossRefGoogle Scholar
[30]Shiu, P.A Brun–Titchmarsh theorem for multiplicative functions. J. Reine Angew. Math. 313 (1980), 161–170.Google Scholar
[31]Silverberg, A.Group order formulas for reductions of CM elliptic curves. Arithmetic, Geometry, Cryptography and Coding Theory 2009. Contemp. Math. 521 (Amer. Math. Soc., Providence, RI, 2010), 107–120.CrossRefGoogle Scholar
[32]Tao, T. Erdős's divisor bound. Blog post published July 23, 2011 at http://terrytao.wordpress.com/2011/07/23/erdos-divisor-bound/. To appear in the forthcoming book Spending Symmetry.Google Scholar
[33]Titchmarsh, E. C.A divisor problem. Rend. Circ. Mat. Palermo 54 (1930), 414–429. Errata in 57 (1933), 478–479.CrossRefGoogle Scholar
[34]Wirsing, E.Das asymptotische Verhalten von Summen über multiplikative Funktionen. Math. Ann. 143 (1961), 75–102.CrossRefGoogle Scholar
[35]Wolke, D.Multiplikative Funktionen auf schnell wachsenden Folgen. J. Reine Angew. Math. 251 (1971), 54–67.Google Scholar