Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-24T18:20:30.827Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCAL SET APPROXIMATION: MATTILA–VUORINEN TYPE SETS, REIFENBERG TYPE SETS, AND TANGENT SETS

Part of: Miscellaneous topics - Partial differential equations Existence theories Classical measure theory Manifolds

Published online by Cambridge University Press:  30 October 2015

MATTHEW BADGER  and
STEPHEN LEWIS
MATTHEW BADGER
Affiliation:
Department of Mathematics, University of Connecticut, Storrs, CT 06269-3009, USA; matthew.badger@uconn.edu
STEPHEN LEWIS
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA 98195-4350, USA; iam@stephen-lewis.net

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the interplay between the local and asymptotic geometry of a set 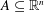$A\subseteq \mathbb{R}^{n}$ and the geometry of model sets 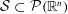${\mathcal{S}}\subset {\mathcal{P}}(\mathbb{R}^{n})$, which approximate 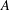$A$ locally uniformly on small scales. The framework for local set approximation developed in this paper unifies and extends ideas of Jones, Mattila and Vuorinen, Reifenberg, and Preiss. We indicate several applications of this framework to variational problems that arise in geometric measure theory and partial differential equations. For instance, we show that the singular part of the support of an 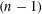$(n-1)$-dimensional asymptotically optimally doubling measure in 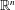$\mathbb{R}^{n}$ (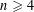$n\geqslant 4$) has upper Minkowski dimension at most 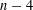$n-4$.

MSC classification

Primary: 49J52: Nonsmooth analysis
Secondary: 28A75: Length, area, volume, other geometric measure theory 35R35: Free boundary problems 49Q20: Variational problems in a geometric measure-theoretic setting
Type
Research Article
Information
Forum of Mathematics, Sigma , Volume 3 , 2015 , e24
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2015

References

Badger, M., ‘Harmonic polynomials and tangent measures of harmonic measure’, Rev. Mat. Iberoam. 27(3) (2011), 841–870.Google Scholar
Badger, M., ‘Flat points in zero sets of harmonic polynomials and harmonic measure from two sides’, J. Lond. Math. Soc. (2) 87(1) (2013), 111–137.Google Scholar
Beer, G., Topologies on Closed and Closed Convex Sets, Mathematics and its Applications, 268 (Kluwer Academic Publishers Group, Dordrecht, 1993).Google Scholar
Cheeger, J. and Colding, T. H., ‘On the structure of spaces with Ricci curvature bounded below. I’, J. Differential Geom. 46(3) (1997), 406–480.Google Scholar
David, G., ‘Hölder regularity of two-dimensional almost-minimal sets in ℝn’, Ann. Fac. Sci. Toulouse Math. (6) 18(1) (2009), 65–246.Google Scholar
David, G., De Pauw, T. and Toro, T., ‘A generalization of Reifenberg’s theorem in ℝ3’, Geom. Funct. Anal. 18(4) (2008), 1168–1235.Google Scholar
David, G., Kenig, C. and Toro, T., ‘Asymptotically optimally doubling measures and Reifenberg flat sets with vanishing constant’, Comm. Pure Appl. Math. 54(4) (2001), 385–449.Google Scholar
David, G. and Semmes, S., Analysis of and on Uniformly Rectifiable Sets, Mathematical Surveys and Monographs, 38 (American Mathematical Society, Providence, RI, 1993).Google Scholar
David, G. and Semmes, S., ‘Fractured fractals and broken dreams’, inSelf-similar Geometry Through Metric and Measure, Oxford Lecture Series in Mathematics and its Applications, 7 (The Clarendon Press, Oxford University Press, New York, 1997).Google Scholar
David, G. and Toro, T., ‘Reifenberg parameterizations for sets with holes’, Mem. Amer. Math. Soc. 215(1012) (2012), vi+102.Google Scholar
Jones, P. W., ‘Rectifiable sets and the traveling salesman problem’, Invent. Math. 102(1) (1990), 1–15.Google Scholar
Kenig, C., Preiss, D. and Toro, T., ‘Boundary structure and size in terms of interior and exterior harmonic measures in higher dimensions’, J. Amer. Math. Soc. 22(3) (2009), 771–796.Google Scholar
Kenig, C. and Toro, T., ‘Free boundary regularity below the continuous threshold: 2-phase problems’, J. Reine Angew. Math. 596 (2006), 1–44.Google Scholar
Kenig, C. E. and Toro, T., ‘Harmonic measure on locally flat domains’, Duke Math. J. 87(3) (1997), 509–551.Google Scholar
Kenig, C. E. and Toro, T., ‘Free boundary regularity for harmonic measures and Poisson kernels’, Ann. of Math. (2) 150(2) (1999), 369–454.Google Scholar
Kirchheim, B. and Preiss, D., ‘Uniformly distributed measures in Euclidean spaces’, Math. Scand. 90(1) (2002), 152–160.Google Scholar
Kowalski, O. and Preiss, D., ‘Besicovitch-type properties of measures and submanifolds’, J. Reine Angew. Math. 379 (1987), 115–151.Google Scholar
Le Donne, E., ‘Metric spaces with unique tangents’, Ann. Acad. Sci. Fenn. Math. 36(2) (2011), 683–694.Google Scholar
Le Donne, E., ‘A metric characeterization of Carnot groups’, Proc. Amer. Math. Soc. 143(2) (2015), 845–849.CrossRefGoogle Scholar
Lewis, J. L. and Nyström, K., ‘Boundary behaviour of p-harmonic functions in domains beyond Lipschitz domains’, Adv. Calc. Var. 1(2) (2008), 133–170.Google Scholar
Lewis, S., ‘Singular points of Hölder asymptotically optimally doubling measures’, Calc. Var. Partial Differential Equations (2015), 47; doi:10.1007/s00526-015-0918-y.Google Scholar
Liang, X., ‘Almgren-minimality of unions of two almost orthogonal planes in ℝ4’, Proc. Lond. Math. Soc. (3) 106(5) (2013), 1005–1059.Google Scholar
Liang, X., ‘Almgren and topological minimality for the set Y× Y’, J. Funct. Anal. 266(10) (2014), 6007–6054.Google Scholar
Luu, T. D., ‘On some properties of three-dimensional minimal sets in ℝ4’, Ann. Fac. Sci. Toulouse Math. (6) 22(3) (2013), 465–493.Google Scholar
Mattila, P. and Vuorinen, M., ‘Linear approximation property, Minkowski dimension, and quasiconformal spheres’, J. Lond. Math. Soc. (2) 42(2) (1990), 249–266.Google Scholar
Mattila, P., ‘Geometry of sets and measures in Euclidean spaces’, inFractals and Rectifiability, Cambridge Studies in Advanced Mathematics, 44 (Cambridge University Press, Cambridge, 1995).Google Scholar
Naber, A. and Valtorta, D., ‘Volume estimates on the critical sets of solutions to elliptic PDEs’, Preprint, 2014. arXiv:1403.4176.Google Scholar
Okikiolu, K., ‘Characterization of subsets of rectifiable curves in Rn’, J. Lond. Math. Soc. (2) 46(2) (1992), 336–348.Google Scholar
Preiss, D., Tolsa, X. and Toro, T., ‘On the smoothness of Hölder doubling measures’, Calc. Var. Partial Differential Equations 35(3) (2009), 339–363.Google Scholar
Preiss, D., ‘Geometry of measures in Rn: distribution, rectifiability, and densities’, Ann. of Math. (2) 125(3) (1987), 537–643.Google Scholar
Reifenberg, E. R., ‘Solution of the Plateau problem for m-dimensional surfaces of varying topological type’, Acta Math. 104 (1960), 1–92.Google Scholar
Tyrrell Rockafellar, R. and Wets, R. J.-B., Variational Analysis, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 317 (Springer, Berlin, 1998).Google Scholar
Taylor, J. E., ‘The structure of singularities in soap-bubble-like and soap-film-like minimal surfaces’, Ann. of Math. (2) 103(3) (1976), 489–539.Google Scholar
Tolsa, X., ‘Uniform measures and uniform rectifiability’, J. Lond. Math. Soc. (2) 92(1) (2015), 1–18.Google Scholar
Toro, T., ‘Geometric conditions and existence of bi-Lipschitz parameterizations’, Duke Math. J. 77(1) (1995), 193–227.Google Scholar
Walkup, D. W. and Wets, R. J.-B., ‘Continuity of some convex-cone-valued mappings’, Proc. Amer. Math. Soc. 18 (1967), 229–235.Google Scholar