Hostname: page-component-8448b6f56d-cfpbc Total loading time: 0 Render date: 2024-04-18T11:07:12.663Z Has data issue: false hasContentIssue false
  • English
  • Français

Cohomology of fiber bunched cocycles over hyperbolic systems

Published online by Cambridge University Press:  04 August 2014

VICTORIA SADOVSKAYA
VICTORIA SADOVSKAYA*
Affiliation:
Department of Mathematics, The Pennsylvania State University, University Park, PA 16802, USA email sadovskaya@psu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider Hölder continuous fiber bunched 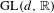$\text{GL}(d,\mathbb{R})$-valued cocycles over an Anosov diffeomorphism. We show that two such cocycles are Hölder continuously cohomologous if they have equal periodic data, and prove a result for cocycles with conjugate periodic data. We obtain a corollary for cohomology between any constant cocycle and its small perturbation. The fiber bunching condition means that non-conformality of the cocycle is dominated by the expansion and contraction in the base. We show that this condition can be established based on the periodic data. Some important examples of cocycles come from the differential of a diffeomorphism and its restrictions to invariant sub-bundles. We discuss an application of our results to the question of whether an Anosov diffeomorphism is smoothly conjugate to a 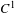$C^{1}$-small perturbation. We also establish Hölder continuity of a measurable conjugacy between a fiber bunched cocycle and a uniformly quasiconformal one. Our main results also hold for cocycles with values in a closed subgroup of 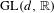$\text{GL}(d,\mathbb{R})$, for cocycles over hyperbolic sets and shifts of finite type, and for linear cocycles on a non-trivial vector bundle.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 8 , December 2015 , pp. 2669 - 2688
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A., Santamaria, J. and Viana, M.. Holonomy invariance: rough regularity and applications to Lyapunov exponents. Astérisque 358 (2013), 13–74.Google Scholar
Barreira, L. and Pesin, Ya.. Nonuniform Hyperbolicity: Dynamics of Systems with Nonzero Lyapunov Exponents (Encyclopedia of Mathematics and Its Applications, 115). Cambridge University Press, Cambridge, 2007.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer-Verlag, Berlin, 1975.CrossRefGoogle Scholar
Goetze, E. and Spatzier, R.. On Livšics theorem, superrigidity, and Anosov actions of semisimple Lie groups. Duke Math. J. 88(1) (1997), 1–27.CrossRefGoogle Scholar
Gogolev, A.. Smooth conjugacy of Anosov diffeomorphisms on higher dimensional tori. J. Modern Dynam. 2(4) (2008), 645–700.CrossRefGoogle Scholar
Gogolev, A., Kalinin, B. and Sadovskaya, V.. Local rigidity for Anosov automorphisms. Math. Res. Lett. 18(5) (2011), 843–858 (appendix by R. de la Llave).CrossRefGoogle Scholar
Kalinin, B.. Livšic theorem for matrix cocycles. Ann. of Math. (2) 173 (2011), 1025–1042.CrossRefGoogle Scholar
Kalinin, B. and Sadovskaya, V.. On local and global rigidity of quasiconformal Anosov diffeomorphisms. J. Inst. Math. Jussieu 2(4) (2003), 567–582.CrossRefGoogle Scholar
Kalinin, B. and Sadovskaya, V.. On Anosov diffeomorphisms with asymptotically conformal periodic data. Ergod. Th. & Dynam. Sys. 29 (2009), 117–136.CrossRefGoogle Scholar
Kalinin, B. and Sadovskaya, V.. Linear cocycles over hyperbolic systems and criteria of conformality. J. Mod. Dynam. 4(3) (2010), 419–441.CrossRefGoogle Scholar
Kalinin, B. and Sadovskaya, V.. Cocycles with one exponent over partially hyperbolic systems. Geometriae Dedicata 167(1) (2013), 167–188.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and Its Applications, 54). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Katok, A. and Nitica, V.. Rigidity in Higher Rank Abelian Group Actions: Volume 1, Introduction and Cocycle Problem. Cambridge University Press, Cambridge, 2011.CrossRefGoogle Scholar
Livšic, A. N.. Homology properties of Y-systems. Math. Zametki 10 (1971), 758–763.Google Scholar
Livšic, A. N.. Cohomology of dynamical systems. Math. USSR Izvestija 6 (1972), 1278–1301.CrossRefGoogle Scholar
de la Llave, R.. Invariants for smooth conjugacy of hyperbolic dynamical systems II. Commun. Math. Phys. 109 (1987), 368–378.CrossRefGoogle Scholar
de la Llave, R.. Smooth conjugacy and SRB measures for uniformly and non-uniformly hyperbolic systems. Comm. Math. Phys. 150 (1992), 289–320.CrossRefGoogle Scholar
de la Llave, R.. Rigidity of higher-dimensional conformal Anosov systems. Ergod. Th. & Dynam. Sys. 22(6) (2002), 1845–1870.CrossRefGoogle Scholar
de la Llave, R.. Further rigidity properties of conformal Anosov systems. Ergod. Th. & Dynam. Sys. 24(5) (2004), 1425–1441.CrossRefGoogle Scholar
de la Llave, R. and Moriyón, R.. Invariants for smooth conjugacy of hyperbolic dynamical systems IV. Commun. Math. Phys. 116 (1988), 185–192.CrossRefGoogle Scholar
de la Llave, R. and Windsor, A.. Livšic theorem for non-commutative groups including groups of diffeomorphisms, and invariant geometric structures. Ergod. Th. & Dynam. Sys. 30(4) (2010), 1055–1100.CrossRefGoogle Scholar
Nicol, M. and Pollicott, M.. Measurable cocycle rigidity for some non-compact groups. Bull. London Math. Soc. 31(5) (1999), 592–600.CrossRefGoogle Scholar
Nitica, V. and Török, A.. Cohomology of dynamical systems and rigidity of partially hyperbolic actions of higher-rank lattices. Duke Math. J. 79(3) (1995), 751–810.CrossRefGoogle Scholar
Nitica, V. and Török, A.. Regularity of the transfer map for cohomologous cocycles. Ergod. Th. & Dynam. Sys. 18(5) (1998), 1187–1209.CrossRefGoogle Scholar
Parry, W.. The Livšic periodic point theorem for non-abelian cocycles. Ergod. Th. & Dynam. Sys. 19(3) (1999), 687–701.CrossRefGoogle Scholar
Parry, W. and Pollicott, M.. The Livšic cocycle equation for compact Lie group extensions of hyperbolic systems. J. Lond. Math. Soc. (2) 56(2) (1997), 405–416.CrossRefGoogle Scholar
Pesin, Ya.. Lectures on Partial Hyperbolicity and Stable Ergodicity (Zurich Lectures in Advanced Mathematics). European Mathematical Society, Zurich, 2004.CrossRefGoogle Scholar
Pollicott, M. and Walkden, C. P.. Livšic theorems for connected Lie groups. Trans. Amer. Math. Soc. 353(7) (2001), 2879–2895.CrossRefGoogle Scholar
Sadovskaya, V.. Cohomology of GL(2, ℝ)-valued cocycles over hyperbolic systems. Discr. Cont. Dynam. Sys. 33(5) (2013), 2085–2104.CrossRefGoogle Scholar
Schmidt, K.. Remarks on Livšic theory for non-abelian cocycles. Ergod. Th. & Dynam. Sys. 19(3) (1999), 703–721.CrossRefGoogle Scholar
Viana, M.. Almost all cocycles over any hyperbolic system have nonvanishing Lyapunov exponents. Ann. of Math. (2) 167(2) (2008), 643–680.CrossRefGoogle Scholar