Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-18T10:57:29.270Z Has data issue: false hasContentIssue false
  • English
  • Français

Structure of transition classes for factor codes on shifts of finite type

Published online by Cambridge University Press:  07 August 2014

MAHSA ALLAHBAKHSHI ,
SOONJO HONG  and
UIJIN JUNG
MAHSA ALLAHBAKHSHI
Affiliation:
Centro de Modelamiento Matemático, Universidad de Chile, Av. Blanco Encalada 2120, Piso 7, Santiago de Chile, Chile email mallahbakhshi@dim.uchile.cl, hsoonjo@dim.uchile.cl
SOONJO HONG
Affiliation:
Centro de Modelamiento Matemático, Universidad de Chile, Av. Blanco Encalada 2120, Piso 7, Santiago de Chile, Chile email mallahbakhshi@dim.uchile.cl, hsoonjo@dim.uchile.cl
UIJIN JUNG
Affiliation:
Department of Mathematics, Ajou University, Suwon 443-749, South Korea email uijin@ajou.ac.kr
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a factor code ${\it\pi}$ from a shift of finite type 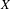$X$ onto a sofic shift $Y$, the class degree of ${\it\pi}$ is defined to be the minimal number of transition classes over the points of $Y$. In this paper, we investigate the structure of transition classes and present several dynamical properties analogous to the properties of fibers of finite-to-one factor codes. As a corollary, we show that for an irreducible factor triple, there cannot be a transition between two distinct transition classes over a right transitive point, answering a question raised by Quas.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 8 , December 2015 , pp. 2353 - 2370
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allahbakhshi, M. and Quas, A.. Class degree and relative maximal entropy. Trans. Amer. Math. Soc. 365(3) (2013), 1347–1368.CrossRefGoogle Scholar
Ashley, J.. Bounded-to-1 factors of an aperiodic shift of finite type are 1-to-1 almost everywhere factors also. Ergod. Th. & Dynam. Sys. 10(4) (1990), 615–625.CrossRefGoogle Scholar
Blackwell, D.. The entropy of functions of finite-state Markov chains. Transactions of the First Prague Conference on Information Theory, Statistical Decision Functions, Random Processes (Liblice, Prague, 28–30 November 1956). Publishing House of the Czechoslovak Academy of Sciences, Prague, 1957, pp. 13–20.Google Scholar
Boyle, M.. Lower entropy factors of sofic systems. Ergod. Th. & Dynam. Sys. 3(4) (1983), 541–557.CrossRefGoogle Scholar
Boyle, M.. Constraints on the degree of a sofic homomorphism and the induced multiplication of measures on unstable sets. Israel J. Math. 53(1) (1986), 52–68.CrossRefGoogle Scholar
Boyle, M. and Petersen, K.. Hidden Markov processes in the context of symbolic dynamics. Entropy of Hidden Markov Processes and Connections to Dynamical Systems (London Mathematical Society Lecture Note Series, 385). Cambridge University Press, Cambridge, 2011, pp. 5–71.CrossRefGoogle Scholar
Boyle, M. and Tuncel, S.. Infinite-to-one codes and Markov measures. Trans. Amer. Math. Soc. 285(2) (1984), 657–684.CrossRefGoogle Scholar
Burke, C. J. and Rosenblatt, M.. A Markovian function of a Markov chain. Ann. Math. Stat. 29 (1958), 1112–1122.CrossRefGoogle Scholar
Chazottes, J.-R. and Ugalde, E.. Projection of Markov measures may be Gibbsian. J. Stat. Phys. 111(5-6) (2003), 1245–1272.CrossRefGoogle Scholar
Coven, E. M. and Paul, M. E.. Endomorphisms of irreducible subshifts of finite type. Math. Systems Theory 8(2) (1974/75), 167–175.CrossRefGoogle Scholar
Gatzouras, D. and Peres, Y.. Invariant measures of full dimension for some expanding maps. Ergod. Th. & Dynam. Sys. 17(1) (1997), 147–167.CrossRefGoogle Scholar
Hedlund, G. A.. Endomorphisms and automorphisms of the shift dynamical system. Math. Systems Theory 3 (1969), 320–375.CrossRefGoogle Scholar
Jung, U.. Fiber-mixing codes and factors of Gibbs measures for shifts of finite type. Preprint, 2013.Google Scholar
Kitchens, B., Marcus, B. and Trow, P.. Eventual factor maps and compositions of closing maps. Ergod. Th. & Dynam. Sys. 11(1) (1991), 85–113.CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Petersen, K., Quas, A. and Shin, S.. Measures of maximal relative entropy. Ergod. Th. & Dynam. Sys. 23(1) (2003), 207–223.CrossRefGoogle Scholar
Shin, S.. Pseudo-cyclic renewal systems. Theoret. Comput. Sci. 412(39) (2011), 5387–5399.CrossRefGoogle Scholar
Thomsen, K.. On the structure of a sofic shift space. Trans. Amer. Math. Soc. 356(9) (2004), 3557–3619.CrossRefGoogle Scholar
Trow, P.. Degrees of finite-to-one factor maps. Israel J. Math. 71(2) (1990), 229–238.CrossRefGoogle Scholar
Walters, P.. Relative pressure, relative equilibrium states, compensation functions and many-to-one codes between subshifts. Trans. Amer. Math. Soc. 296(1) (1986), 1–31.CrossRefGoogle Scholar
Yoo, J.. On factor maps that send Markov measures to Gibbs measures. J. Stat. Phys. 141(6) (2010), 1055–1070.CrossRefGoogle Scholar
Yoo, J.. Measures of maximal relative entropy with full support. Ergod. Th. & Dynam. Sys. 31(6) (2011), 1889–1899.CrossRefGoogle Scholar