Hostname: page-component-8448b6f56d-tj2md Total loading time: 0 Render date: 2024-04-16T21:40:17.076Z Has data issue: false hasContentIssue false
  • English
  • Français

Effects of inertia and viscoelasticity on sedimenting anisotropic particles

Published online by Cambridge University Press:  30 July 2015

Vivekanand Dabade ,
Navaneeth K. Marath  and
Ganesh Subramanian
Vivekanand Dabade
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore 560064, India Department of Aerospace Engineering and Mechanics, University of Minnesota, Minneapolis, MN 55455, USA
Navaneeth K. Marath
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore 560064, India
Ganesh Subramanian*
Affiliation:
Engineering Mechanics Unit, Jawaharlal Nehru Centre for Advanced Scientific Research, Jakkur, Bangalore 560064, India
*
†Email address for correspondence: sganesh@jncasr.ac.in
Get access Rights & Permissions [Opens in a new window]

Abstract

An axisymmetric particle sedimenting in an otherwise quiescent Newtonian fluid, in the Stokes regime, retains its initial orientation. For the special case of a spheroidal geometry, we examine analytically the effects of weak inertia and viscoelasticity in driving the particle towards an eventual steady orientation independent of initial conditions. The generalized reciprocal theorem, together with a novel vector spheroidal harmonics formalism, is used to find closed-form analytical expressions for the 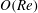$O(\mathit{Re})$ inertial torque and the 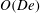$O(\mathit{De})$ viscoelastic torque acting on a sedimenting spheroid of an arbitrary aspect ratio. Here, 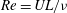$\mathit{Re}=UL/{\it\nu}$ is the Reynolds number, with 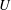$U$ being the sedimentation velocity, 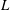$L$ the semi-major axis and ${\it\nu}$ the fluid kinematic viscosity, and is a measure of the inertial forces acting at the particle scale. The Deborah number, 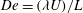$\mathit{De}=({\it\lambda}U)/L$, is a dimensionless measure of the fluid viscoelasticity, with 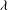${\it\lambda}$ being the intrinsic relaxation time of the underlying microstructure. The analysis is valid in the limit 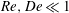$\mathit{Re},\mathit{De}\ll 1$, and the effects of viscoelasticity are therefore modelled using the constitutive equation of a second-order fluid. The inertial torque always acts to turn the spheroid broadside-on, while the final orientation due to the viscoelastic torque depends on the ratio of the magnitude of the first (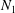$N_{1}$) to the second normal stress difference (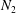$N_{2}$), and the sign (tensile or compressive) of 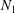$N_{1}$. For the usual case of near-equilibrium complex fluids – a positive and dominant 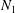$N_{1}$ (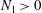$N_{1}>0$, 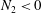$N_{2}<0$ and 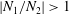$|N_{1}/N_{2}|>1$) – both prolate and oblate spheroids adopt a longside-on orientation. The viscoelastic torque is found to be remarkably sensitive to variations in ${\it\kappa}$ in the slender-fibre limit (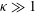${\it\kappa}\gg 1$), where 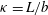${\it\kappa}=L/b$ is the aspect ratio, 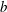$b$ being the radius of the spheroid (semi-minor axis). The angular dependence of the inertial and viscoelastic torques turn out to be identical, and one may then characterize the long-time orientation of the sedimenting spheroid based solely on a critical value (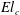$\mathit{El}_{c}$) of the elasticity number, 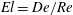$\mathit{El}=\mathit{De}/\mathit{Re}$. For 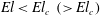$\mathit{El}<\mathit{El}_{c}~({>}\mathit{El}_{c})$, inertia (viscoelasticity) prevails with the spheroid settling broadside-on (longside-on). The analysis shows that 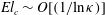$\mathit{El}_{c}\sim O[(1/\text{ln}\,{\it\kappa})]$ for 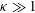${\it\kappa}\gg 1$, and the viscoelastic torque thus dominates for a slender rigid fibre. For a slender fibre alone, we also briefly analyse the effects of elasticity on fibre orientation outside the second-order fluid regime.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Non-Newtonian Flows: Non-Newtonian Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 778 , 10 September 2015 , pp. 133 - 188
Copyright
© 2015 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arigo, M. T., Rajagopalan, D., Shapley, N. & Mckinley, G. H. 1995 The sedimentation of a sphere through an elastic fluid. Part 1. Steady motion. J. Non-Newtonian Fluid Mech. 60, 225–257.CrossRefGoogle Scholar
Batchelor, G. K. 1970 Slender-body theory for particles of arbitrary cross-section in Stokes flow. J. Fluid Mech. 44 (03), 419–440.CrossRefGoogle Scholar
Batchelor, G. K. 1971 The stress generated in a non-dilute suspension of elongated particles by pure straining motion. J. Fluid Mech. 46, 813–829.CrossRefGoogle Scholar
Berker, R. 1964 Contrainte sur une paroi en contact avec un fluide visqueux classique un fluide de Stokes un fluide de Coleman–Noll. C. R. Acad. Sci. Paris 258 (21), 5144–5147.Google Scholar
Binous, H. & Phillips, R. J. 1993 Dynamic simulation of one and two particles sedimenting in viscoelastic suspensions of FENE dumbbells. J. Non-Newtonian Fluid Mech. 83, 93–130.CrossRefGoogle Scholar
Bird, R. B., Armstrong, R. C. & Hassager, O. 1987 Dynamics of Polymeric Liquids. vol. 1. Wiley.Google Scholar
Boyer, F., Pouliquen, O. & Guazzelli, E. 2011 Dense suspensions in rotating-rod flows: normal stresses and particle migration. J. Fluid Mech. 686, 5–25.CrossRefGoogle Scholar
Brady, J. F. & Bossis, G. 1988 Stokesian dynamics. Annu. Rev. Fluid Mech. 20, 111–157.CrossRefGoogle Scholar
Brady, J. F. & Vicic, M. 1995 Normal stresses in colloidal dispersions. J. Rheol. 39, 545–566.CrossRefGoogle Scholar
Brenner, H. 1961 The Oseen resistance of a particle of arbitrary shape. J. Fluid Mech. 11 (04), 604–610.CrossRefGoogle Scholar
Brenner, H. 1966 Hydrodynamic resistance of particles at small Reynolds numbers. Adv. Chem. Engng 6, 287–438.CrossRefGoogle Scholar
Brenner, H. & Condiff, D.W. 1974 Transport mechanics in systems of orientable particles. IV. Convective transport. J. Colloid Interface Sci. 47 (1), 199–264.CrossRefGoogle Scholar
Brunn, P. 1977 The slow motion of a rigid particle in a second-order fluid. J. Fluid Mech. 82 (3), 529–550.CrossRefGoogle Scholar
Butler, J. E. & Shaqfeh, E. S. G. 2002 Dynamic simulations of the inhomogeneous sedimentation of rigid fibers. J. Fluid Mech. 468, 205–237.CrossRefGoogle Scholar
Caflisch, R. E. & Luke, J. H. C. 1985 Variance in the sedimentation speed of a suspension. Phys. Fluids 28, 759–760.CrossRefGoogle Scholar
Caro, C. G., Pedley, T. J., Schroter, R. C. & Seed, W. A. 2012 The Mechanics of the Circulation. Cambridge University Press.Google Scholar
Caswell, B. & Schwarz, W. H. 1962 The creeping motion of a non-Newtonian fluid past a sphere. J. Fluid Mech. 13, 417–426.CrossRefGoogle Scholar
Chiba, K., Song, K.-W. & Horikawa, A. 1986 Motion of a slender body in quiescent polymer solutions. Rheol. Acta 25 (4), 380–388.CrossRefGoogle Scholar
Chilcott, M. D. & Rallison, J. M. 1988 Creeping flow of dilute polymer solutions past cylinders and spheres. J. Non-Newtonian Fluid Mech. 29, 381–432.CrossRefGoogle Scholar
Cho, K., Cho, Y. I. & Park, N. A. 1992 Hydrodynamics of a vertically falling thin cylinder in non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 45 (1), 105–145.CrossRefGoogle Scholar
Cho, H. R., Iribarne, J. V. & Richards, W. G. 1981 On the orientation of ice crystals in a cumulonimbus cloud. J. Atmos. Sci. 38, 1111–1114.2.0.CO;2>CrossRefGoogle Scholar
Chwang, A. T. 1975 Hydromechanics of low-Reynolds-number flow. Part 3. Motion of a spheroidal particle in quadratic flows. J. Fluid Mech. 72, 17–34.CrossRefGoogle Scholar
Chwang, A. T. & Wu, T. Y.-T. 1974 Hydromechanics of low-Reynolds-number flow. Part 1. Rotation of axisymmetric prolate bodies. J. Fluid Mech. 63, 607–622.CrossRefGoogle Scholar
Chwang, A. T. & Wu, T. Y.-T. 1975 Hydromechanics of low-Reynolds-number flow. Part 2. Singularity method for Stokes flows. J. Fluid Mech. 67, 787–815.CrossRefGoogle Scholar
Claeys, I. L. & Brady, J. F. 1993a Suspensions of prolate spheroids in Stokes flow. Part 2. Statistically homogeneous dispersions. J. Fluid Mech. 251, 443–477.CrossRefGoogle Scholar
Claeys, I. L. & Brady, J. F. 1993b Suspensions of prolate spheroids in Stokes flow. Part 1. Dynamics of a finite number of particles in an unbounded fluid. J. Fluid Mech. 251, 411–442.CrossRefGoogle Scholar
Claeys, I. L. & Brady, J. F. 1993c Suspensions of prolate spheroids in Stokes flow. Part 3. Hydrodynamic transport properties of crystalline dispersions. J. Fluid Mech. 251, 479–500.CrossRefGoogle Scholar
Cox, R. G. 1965 The steady motion of a particle of arbitrary shape at small Reynolds numbers. J. Fluid Mech. 23, 625–643.CrossRefGoogle Scholar
Cox, R. G. 1970 The motion of long slender bodies in a viscous fluid. Part I. General theory. J. Fluid Mech. 44, 791–810.CrossRefGoogle Scholar
Dabade, V., Marath, N. K. & Subramanian, G. 2015 The effect of inertia on the orientation dynamics of spheroidal particles in simple shear flow. J. Fluid Mech. (submitted).Google Scholar
Feng, J. F., Joseph, D. D., Glowinski, R. & Pan, T. W. 1995 A three-dimensional computation of the force and torque on an ellipsoid settling slowly through viscoelastic fluid. J. Fluid Mech. 283, 1–16.CrossRefGoogle Scholar
Fortes, A. F., Joseph, D. D. & Lundgren, T. S. 1987 Nonlinear mechanics of fluidization of beds of spherical particles. J. Fluid Mech. 177, 467–483.CrossRefGoogle Scholar
Galdi, G. P. 2000 Slow steady fall of rigid bodies in a second-order fluid. J. Non-Newtonian Fluid Mech. 90, 81–89.CrossRefGoogle Scholar
Galdi, G. P., Vaidya, A., Pokorny, M., Daniel, D. D. J. & Feng, J. 2002 Orientation of symmetric bodies falling in a second-order liquid at non-zero Reynolds number. Math. Models Meth. Appl. Sci. 12, 1653–1690.CrossRefGoogle Scholar
Garrett, T. J., Gerber, H., Baumgardner, D. G., Twohy, C. H. & Weinstock, E. M. 2003 Small highly reflective ice crystals in low-latitude cirrus. Geophys. Res. Lett. 30, 12,1–4.CrossRefGoogle Scholar
Harlen, O. G. 1990 High-Deborah-number flow of a dilute polymer solution past a sphere falling along the axis of a cylindrical tube. J. Non-Newtonian Fluid Mech. 37 (2), 157–173.CrossRefGoogle Scholar
Harlen, O. G. & Koch, D. L. 1993 Simple shear flow of a suspension of fibers in a dilute polymer solution. J. Fluid Mech. 252, 187–207.CrossRefGoogle Scholar
Harlen, O. G., Rallison, J. M. & Chilcott, M. D. 1990 High-Deborah-number flows of dilute polymer solutions. J. Non-Newtonian Fluid Mech. 34 (3), 319–349.CrossRefGoogle Scholar
Herzhaft, B. & Guazzelli, E. 1999 Experimental study of the sedimentation of dilute and semi-dilute suspensions of fibers. J. Fluid Mech. 384, 133–158.CrossRefGoogle Scholar
Herzhaft, H. B., Hinch, E. J., Nicolai, O. L. & Guazzelli, E. 1995 Particle velocity fluctuations and hydrodynamic self-diffusion of sedimenting non-Brownian spheres. Phys. Fluids 7 (1), 12–23.Google Scholar
Hinch, E. J. 2011 The measurement of suspension rheology. J. Fluid Mech. 686, 1–4.CrossRefGoogle Scholar
Hinch, E. J. & Leal, L. G. 1972 The effect of Brownian motion on the rheological properties of a suspension of non-spherical particles. J. Fluid Mech. 52, 683–712.CrossRefGoogle Scholar
Hogan, R. J., Tian, L., Brown, P. R. A., Westbrook, C. D., Heymsfield, A. J. & Eastment, J. D. 2012 Radar scattering from ice aggregates using the horizontally aligned oblate spheroid approximation. J. Appl. Meteorol. Climatol. 51, 655–671.CrossRefGoogle Scholar
Jeffery, G. B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. A 102, 161–179.Google Scholar
Joseph, D. D. 1990 Fluid Dynamics of Viscoelastic Liquids. vol. 84. Springer.CrossRefGoogle Scholar
Joseph, D. D. & Liu, Y. J. 1993 Bingham award lecture – orientation of long bodies falling in a viscoelastic liquid. J. Rheol. 37, 961–983.CrossRefGoogle Scholar
Keentok, M., Georgescu, A. G., Sherwood, A. A. & Tanner, R. I. 1980 The measurement of the second normal stress difference for some polymer solutions. J. Non-Newtonian Fluid Mech. 6 (3), 303–324.CrossRefGoogle Scholar
Khayat, R. E. & Cox, R. G. 1989 Inertia effects on the motion of long slender bodies. J. Fluid Mech. 209, 435–462.CrossRefGoogle Scholar
Kim, S. J. 1985a A note on Faxen laws for non-spherical particles. Intl J. Multiphase Flow 11 (5), 713–719.CrossRefGoogle Scholar
Kim, S. J. 1985b Sedimentation of two arbitrarily oriented spheroids in a viscous fluid. Intl J. Multiphase Flow 11 (5), 699–712.CrossRefGoogle Scholar
Kim, S. 1986a The motion of ellipsoids in a second order fluid. J. Non-Newtonian Fluid Mech. 21 (2), 255–269.CrossRefGoogle Scholar
Kim, S. J. 1986b Singularity solutions for ellipsoids in low-Reynolds-number flows: with applications to the calculation of hydrodynamic interactions in suspensions of ellipsoids. Intl J. Multiphase Flow 12 (3), 469–491.CrossRefGoogle Scholar
Kim, S. J. & Arunachalam, P. V. 1987 The general solution for an ellipsoid in low-Reynolds-number flow. J. Fluid Mech. 178, 535–547.CrossRefGoogle Scholar
Kim, S. & Karrila, S. J. 1991 Microhydrodynamics: Principles and Selected Applications. Butterworth-Heinemann.Google Scholar
Klett, J. D. 1995 Orientation model for particles in turbulence. J. Atmos. Sci. 52, 2276–2285.2.0.CO;2>CrossRefGoogle Scholar
Koch, D. L. & Shaqfeh, E. S. G. 1989 The instability of a dispersion of sedimenting spheroids. J. Fluid Mech. 209, 521–542.CrossRefGoogle Scholar
Koch, D. L. & Shaqfeh, E. S. G. 1991 Screening in sedimenting suspensions. J. Fluid Mech. 224, 275–303.CrossRefGoogle Scholar
Koch, D. L. & Subramanian, G. 2006 The stress in a dilute suspension of spheres suspended in a second-order fluid subject to a linear velocity field. J. Non-Newtonian Fluid Mech. 138, 87–97.CrossRefGoogle Scholar
Koyaguchi, T., Hallworth, M. A., Huppert, H. E. & Sparks, R. S. J. 1990 Sedimentation of particles from a convecting fluid. Nature 343, 447–450.CrossRefGoogle Scholar
Kushch, V. I. 1995 Addition theorems of partial vector solutions of the Lame equation in a spheroidal basis. Intl Appl. Mech. 31 (2), 155–159.CrossRefGoogle Scholar
Kushch, V. I. 1997 Microstresses and effective elastic moduli of a solid reinforced by periodically distributed spheroidal particles. Intl J. Solids Struct. 34, 1353–1366.CrossRefGoogle Scholar
Kushch, V. I. 1998 Elastic equilibrium of a medium containing a finite number of arbitrarily oriented spheroidal inclusions. Intl J. Solids Struct. 35, 1187–1198.CrossRefGoogle Scholar
Kushch, V. I. & Sangani, A. S. 2000 Stress intensity factor and effective stiffness of a solid containing aligned penny-shaped cracks. Intl J. Solids Struct. 37, 6555–6570.CrossRefGoogle Scholar
Kushch, V. I. & Sevostianov, I. 2004 Effective elastic properties of the particulate composite with transversely isotropic phases. Intl J. Solids Struct. 41, 885–906.CrossRefGoogle Scholar
Larson, R. G. 1988 Constitutive Equations for Polymer Melts and Solutions. Butterworths.Google Scholar
Leal, L. G. 1975 The slow motion of slender rod-like particles in a second-order fluid. J. Fluid Mech. 69, 305–337.CrossRefGoogle Scholar
Leal, L. G. 1979 The motion of small particles in non-Newtonian fluids. J. Non-Newtonian Fluid Mech. 5, 33–78.CrossRefGoogle Scholar
Leal, L. G. & Hinch, E. J. 1971 The effect of weak Brownian rotations on particles in shear flow. J. Fluid Mech. 46, 685–703.CrossRefGoogle Scholar
Leal, L. G. 1992 Laminar Flow and Convective Transport Processes, Scaling Principles and Asymptotic Analysis, Butterworth-Heinemann Series in Chemical Engineering. Butterworth-Heinemann.Google Scholar
Li, L., Manikantan, H., Saintillan, D. & Spagnolie, S. E. 2013 The sedimentation of flexible filaments. J. Fluid Mech. 735, 705–736.CrossRefGoogle Scholar
Liu, Y. J. & Joseph, D. D. 1993 Sedimentation of particles in polymer solutions. J. Fluid Mech. 255, 565–595.CrossRefGoogle Scholar
Loewenberg, M. & Hinch, E. J. 1996 Numerical simulation of a concentrated emulsion in shear flow. J. Fluid Mech. 321, 395–419.CrossRefGoogle Scholar
McKinley, G. H. 2002 Steady and transient motion of spherical particles in viscoelastic liquids. In Transport Processes in Bubble, Drops, and Particles, pp. 338–375. CRC Press.Google Scholar
Morse, P. M. & Feshbach, H. 1953 Methods of Theoretical Physics. McGraw-Hill.Google Scholar
Raja, R. V., Subramanian, G. & Koch, D. L. 2010 Inertial effects on the rheology of a dilute emulsion. J. Fluid Mech. 646, 255–296.CrossRefGoogle Scholar
Rallision, J. M. & Hinch, E. J. 1988 Do we understand the physics in the constitutive equation. J. Non-Newtonian Fluid Mech. 29, 37–55.CrossRefGoogle Scholar
Rallison, J. M. & Hinch, E. J. 2004 The flow of an Oldroyd fluid past a re-entrant corner: the downstream boundary layer. J. Non-Newtonian Fluid Mech. 116, 141–162.CrossRefGoogle Scholar
Ramanathan, V., Barkstrom, B. R. & Harrison, E. F. 1989 Climate and the Earth’s radiation budget. Intl Agrophys. 5, 171–181.Google Scholar
Ramanathan, V. & Saintillan, D. 2012 Concentration instability of sedimenting spheres in a second-order fluid. Phys. Fluids 24, 073302.Google Scholar
Saintillan, D. 2010 The dilute rheology of swimming suspensions: a simple kinetic model. Expl Mech. 50 (9), 1275–1281.CrossRefGoogle Scholar
Saintillan, D., Shaqfeh, E. S. G. & Darve, E. 2006 The growth of concentration fluctuations in dilute dispersions of orientable and deformable particles under sedimentation. J. Fluid Mech. 553, 347–388.CrossRefGoogle Scholar
Sangani, A. S. & Mo, G. 1994 A method for computing Stokes flow interactions among spherical objects and its application to suspensions of drops and porous particles. Phys. Fluids 6 (5), 1637–1652.Google Scholar
Schowalter, W. R., Chaffey, C. E. & Brenner, H. 1968 Rheological behaviour of a dilute emulsion. J. Colloid Interface Sci. 26, 152–160.CrossRefGoogle ScholarPubMed
Schwindinger, K. R. 1999 Particle dynamics and aggregation of crystals in a magma chamber with application to Kilauea Iki olivines. J. Volcanol. Geotherm. Res. 88, 209–238.CrossRefGoogle Scholar
Shatz, L. F. 2004 Singularity method for oblate and prolate spheroids in Stokes and linearized oscillatory flow. Phys. Fluids 16 (3), 664–677.CrossRefGoogle Scholar
Shaqfeh, M. B., Mackaplow, E. S. G. & Schiek, R. L. 1994 A numerical study of heat and mass-transport in fiber suspensions. Proc. R. Soc. 447, 77–110.Google Scholar
Shin, M., Koch, D. L. & Subramanian, G. 2006 A pseudospectral method to evaluate the fluid velocity produced by an array of translating slender fibers. Phys. Fluids 18, 063301.CrossRefGoogle Scholar
Shin, M., Koch, D. L. & Subramanian, G. 2009 Structure and dynamics of dilute suspensions of finite-Reynolds-number settling fibers. Phys. Fluids 21, 123304.CrossRefGoogle Scholar
Subramanian, G. & Koch, D. L. 2005 Inertial effects on fibre motion in simple shear flow. J. Fluid Mech. 535, 383–414.CrossRefGoogle Scholar
Subramanian, G. & Koch, D. L. 2006 Inertial effects on the orientation of nearly spherical particles in simple shear flow. J. Fluid Mech. 557, 257–296.CrossRefGoogle Scholar
Subramanian, G. & Koch, D. L. 2007 Heat transfer from a neutrally buoyant sphere in a second-order fluid. J. Non-Newtonian Fluid Mech. 144 (1), 49–57.CrossRefGoogle Scholar
Tanner, R. I. 2000 Engineering Rheology. Oxford University Press.CrossRefGoogle Scholar
Tee, P. J., Weitz, D. A., Shraiman, B. I., Mucha, P. & Brenner, M. P. 2004 A model for velocity fluctuations in sedimentation. J. Fluid Mech. 501, 71–104.Google Scholar
Vlahovska, P., Blawzdziewicz, J. & Loewenberg, M. 2000 Rheology of a dilute emulsion of surfactant-covered spherical drops. Physica A 276, 50–85.Google Scholar
Vlahovska, P., Blawzdziewicz, J. & Loewenberg, M. 2002 Nonlinear rheology of a dilute emulsion of surfactant-covered spherical drops in time-dependent flows. J. Fluid Mech. 463, 1–24.CrossRefGoogle Scholar
Vlahovska, P. M. & Garica, R. S. 2007 Dynamics of a viscous vesicle in linear flows. Phys. Rev. E 75, 016313.CrossRefGoogle ScholarPubMed
Wang, J. & Joseph, D. D. 2004 Potential flow of a second-order fluid over a sphere or an ellipse. J. Fluid Mech. 511, 201–215.CrossRefGoogle Scholar
Xu, X. & Nadim, A. 1994 Deformation and orientation of an elastic slender body sedimenting in a viscous liquid. Phys. Fluids 6 (9), 2889–2893.CrossRefGoogle Scholar