Hostname: page-component-8448b6f56d-c4f8m Total loading time: 0 Render date: 2024-04-16T04:03:58.340Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral analogues of the law of the wall, the defect law and the log law

Published online by Cambridge University Press:  19 September 2014

Carlo Zúñiga Zamalloa ,
Henry Chi-Hin Ng ,
Pinaki Chakraborty  and
Gustavo Gioia
Carlo Zúñiga Zamalloa
Affiliation:
Okinawa Institute of Science and Technology, 1919-1 Tancha, Onna, Kunigami, Okinawa, 904-0495, Japan Department of Mechanical Science and Engineering, University of Illinois at Urbana-Champaign, Urbana, IL 61801, USA
Henry Chi-Hin Ng
Affiliation:
Okinawa Institute of Science and Technology, 1919-1 Tancha, Onna, Kunigami, Okinawa, 904-0495, Japan
Pinaki Chakraborty*
Affiliation:
Okinawa Institute of Science and Technology, 1919-1 Tancha, Onna, Kunigami, Okinawa, 904-0495, Japan
Gustavo Gioia
Affiliation:
Okinawa Institute of Science and Technology, 1919-1 Tancha, Onna, Kunigami, Okinawa, 904-0495, Japan
*
†Email address for correspondence: pinaki@oist.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Unlike the classical scaling relations for the mean-velocity profiles of wall-bounded uniform turbulent flows (the law of the wall, the defect law and the log law), which are predicated solely on dimensional analysis and similarity assumptions, scaling relations for the turbulent-energy spectra have been informed by specific models of wall turbulence, notably the attached-eddy hypothesis. In this paper, we use dimensional analysis and similarity assumptions to derive three scaling relations for the turbulent-energy spectra, namely the spectral analogues of the law of the wall, the defect law and the log law. By design, each spectral analogue applies in the same spatial domain as the attendant scaling relation for the mean-velocity profiles: the spectral analogue of the law of the wall in the inner layer, the spectral analogue of the defect law in the outer layer and the spectral analogue of the log law in the overlap layer. In addition, as we are able to show without invoking any model of wall turbulence, each spectral analogue applies in a specific spectral domain (the spectral analogue of the law of the wall in the high-wavenumber spectral domain, where viscosity is active, the spectral analogue of the defect law in the low-wavenumber spectral domain, where viscosity is negligible, and the spectral analogue of the log law in a transitional intermediate-wavenumber spectral domain, which may become sizable only at ultra-high 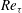$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\mathit{Re}_{\tau }$), with the implication that there exist model-independent one-to-one links between the spatial domains and the spectral domains. We test the spectral analogues using experimental and computational data on pipe flow and channel flow.

JFM classification

Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 498 - 513
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of energy spectra in turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Barenblatt, G. I. 1993 Scaling laws for fully developed turbulent shear flows. Part 1. Basic hypotheses and analysis. J. Fluid Mech. 248, 513–520.CrossRefGoogle Scholar
Barenblatt, G. I. 2003 Scaling (Cambridge Texts in Applied Mathematics, vol. 34) , Cambridge University Press.CrossRefGoogle Scholar
Gioia, G., Guttenberg, N., Goldenfeld, N. & Chakraborty, P. 2010 Spectral theory of the turbulent mean-velocity profile. Phys. Rev. Lett. 105 (18), 184501.CrossRefGoogle ScholarPubMed
Hoyas, S. & Jiménez, J. 2006 Scaling of velocity fluctuations in turbulent channel flows up to ${\mathrm{Re}}_{\tau }=2003$ . Phys. Fluids 18, 011702.Google Scholar
McKeon, B. J. & Morrison, J. F. 2007 Asymptotic scaling in turbulent pipe flow. Phil. Trans. R. Soc. A 365, 771–787.Google Scholar
Morrison, J., McKeon, B., Jiang, W. & Smits, A. 2004 Scaling of the streamwise velocity component in turbulent pipe flow. J. Fluid Mech. 508, 99–131.Google Scholar
Ng, H. C. H., Monty, J. P., Hutchins, N., Chong, M. S. & Marusic, I. 2011 Comparison of turbulent channel and pipe flows with varying Reynolds number. Exp. Fluids 51, 1261–1281.Google Scholar
Perry, A. E. & Chong, M. S. 1982 On the mechanism of wall turbulence. J. Fluid Mech. 119, 173–217.Google Scholar
Perry, A. E., Henbest, S. & Chong, M. S. 1986 A theoretical and experimental study of wall turbulence. J. Fluid Mech. 165, 163–199.CrossRefGoogle Scholar
Perry, A. & Marusic, I. 1995 A wall-wake model for the turbulence structure of boundary layers. Part 1. Extension of the attached eddy hypothesis. J. Fluid Mech. 298, 361–388.CrossRefGoogle Scholar
Rosenberg, B. J., Hultmark, M., Vallikivi, M., Bailey, S. C. C. & Smits, A. J. 2013 Turbulence spectra in smooth- and rough-wall pipe flow at extreme Reynolds numbers. J. Fluid Mech. 731, 46–63.CrossRefGoogle Scholar
Smits, A., McKeon, B. J. & Marusic, I. 2011 High-Reynolds number wall turbulence. Annu. Rev. Fluid Mech. 43, 353–375.CrossRefGoogle Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT Press.Google Scholar
Supplementary material: PDF

Zúñiga Zamalloa supplementary material

Supplementary material

Download Zúñiga Zamalloa supplementary material(PDF)
PDF 1.3 MB