Hostname: page-component-8448b6f56d-42gr6 Total loading time: 0 Render date: 2024-04-16T19:18:27.432Z Has data issue: false hasContentIssue false
  • English
  • Français

The elemental shear dynamo

Published online by Cambridge University Press:  17 April 2012

James C. McWilliams
James C. McWilliams*
Affiliation:
Department of Atmospheric and Oceanic Sciences, University of California, Los Angeles, CA 90095-1565, USA
*
†Email address for correspondence: jcm@atmos.ucla.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A quasi-linear theory is presented for how randomly forced, barotropic velocity fluctuations cause an exponentially growing, large-scale (mean) magnetic dynamo in the presence of a uniform parallel shear flow. It is a ‘kinematic’ theory for the growth of the mean magnetic energy from a small initial seed, neglecting the saturation effects of the Lorentz force. The quasi-linear approximation is most broadly justifiable by its correspondence with computational solutions of nonlinear magnetohydrodynamics, and it is rigorously derived in the limit of small magnetic Reynolds number, 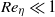. Dynamo action occurs even without mean helicity in the forcing or flow, but random helicity variance is then essential. In a sufficiently large domain and with a small seed wavenumber in the direction perpendicular to the mean shearing plane, a positive exponential growth rate 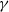can occur for arbitrary values of 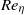, viscous Reynolds number 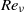, and random-force correlation time 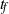and orientation angle 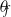in the shearing plane. The value of 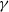is independent of the domain size. The shear dynamo is ‘fast’, with finite 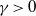in the limit of 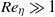. Averaged over random realizations of the forcing history, the ensemble-mean magnetic field grows more slowly, if at all, compared to the r.m.s. field (magnetic energy). In the limit of small 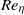and 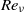, the dynamo behaviour is related to the well-known alpha–omega ansatz when the force is slowly varying (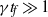) and to the ‘incoherent’ alpha–omega ansatz when the force is more rapidly fluctuating.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory MHD and Electrohydrodynamics: MHD turbulence Waves/Free-surface Flows: Shear waves
Type
Papers
Information
Journal of Fluid Mechanics , Volume 699 , 25 May 2012 , pp. 414 - 452
Copyright
Copyright © Cambridge University Press 2012 The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution-NonCommercial-ShareAlike licence <http://creativecommons.org/licenses/by-nc-sa/2.5/>. The written permission of Cambridge University Press must be obtained for commercial re-use.

References

1. Brandenburg, A., Nordlund, A., Stein, R. F. & Torkelsson, U. 1995 Dynamo-generated turbulence and large-scale magnetic fields in a Keplerian shear. Astrophys. J. 446, 741–754.CrossRefGoogle Scholar
2. Brandenburg, A. & Subramanian, K. 2005 Astrophysical magnetic fields and nonlinear dynamo theory. Phys. Rep. 417, 1–209.CrossRefGoogle Scholar
3. Brown, B. P., Browning, M. K., Brun, A. S., Miesch, M. S. & Toomre, J. 2010 Persistent magnetic wreaths in a rapidly rotating sun. Astrophys. J. 711, 424–438.CrossRefGoogle Scholar
4. Gilbert, A. D., Soward, A. M. & Childress, S. 1997 A fast dynamo of -type. Geophys. Astropys. Fluid Dyn. 85, 293–314.Google Scholar
5. Heinemann, T., McWilliams, J. C. & Schekochihin, A. 2011 Magnetic field generation by randomly forced shearing waves. Phys. Rev. Lett. 107, 255004.CrossRefGoogle ScholarPubMed
6. van Kampen, N. 2007 Stochastic Processes in Physics and Chemistry, 3rd edn. Elsevier.Google Scholar
7. Krause, F. & Radler, K. H. 1980 Mean-Field Magnetohydrodynamics and Dynamo Theory. Pergamon.Google Scholar
8. Kulsrud, R. H. 2010 The origin of our galatic magnetic field. Astron. Nachr. 331, 22–26.CrossRefGoogle Scholar
9. Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
10. Parker, E. N. 1955 Hydromagnetic dynamo models. Astrophys. J. 122, 293–314.CrossRefGoogle Scholar
11. Parker, E. N. 1971 The generation of magnetic fields in astrophysical bodies. II. The galactic field. Astrophys. J. 163, 255–278.CrossRefGoogle Scholar
12. Roberts, P. H. & Soward, A. M. 1992 Dynamo theory. Annu. Rev. Fluid Mech. 24, 459–512.CrossRefGoogle Scholar
13. Sakuraba, A. & Roberts, P. H. 2009 Generation of a strong magnetic field using uniform heat flux at the surface of the core. Nature Geosci. 2, 802–805.CrossRefGoogle Scholar
14. Schrinner, M., Radler, K.-H., Schmitt, D., Rheinhardt, M. & Crhistensen, U. P. 2007 Mean-field concept and direct numerical simulations of rotating magnetoconvection and the geodynamo. Geophys. Astrophys. Fluid Dyn. 101, 81–116.CrossRefGoogle Scholar
15. Silant’ev, N. A. 2000 Magnetic dyanmo due to turbulent helicity fluctuations. Astron. Astrophys. 364, 339–347.Google Scholar
16. Soward, A. M. 1987 Fast dynamo action in a steady flow. J. Fluid Mech. 180, 267–295.CrossRefGoogle Scholar
17. Sridhar, S. & Subramanian, K. 2009 Nonperturbative quasi-linear approach to the shear dynamo problem. Phys. Rev. E 80, 0066315.CrossRefGoogle Scholar
18. Vishniac, E. & Brandenburg, A. 1997 An incoherent dynamo in accretion disks. Astrophys. J. 475, 263–274.CrossRefGoogle Scholar
19. Yousef, T. A., Heinemann, T., Schekochinin, A. A., Kleeorin, N., Rogachevskii, I., Cowley, S. C. & McWilliams, J. C. 2008a Numerical experiments on dynamo action in sheared and rotating turbulence. Astron. Nachr. 329, 737–749.CrossRefGoogle Scholar
20. Yousef, T. A., Heinemann, T., Schekochinin, A. A., Kleeorin, N., Rogachevskii, I., Iskakov, A. B., Cowley, S. C. & McWilliams, J. C. 2008b Generation of magnetic field by combined action of turbulence and shear. Phys. Rev. Lett. 100, 184501.CrossRefGoogle ScholarPubMed