1. Introduction
Spatial localisation is proving to be key to understanding various coherent features seen in fluids comprising Taylor–Couette flow (Abshagen et al. Reference Abshagen, Heise, Pfister and Mullin2010), plane Couette flow (Schneider, Gibson & Burke Reference Schneider, Gibson and Burke2010; Chantry & Kerswell Reference Chantry and Kerswell2014), binary fluid convection (Moses, Fineberg & Steinberg Reference Moses, Fineberg and Steinberg1987; Batiste et al. Reference Batiste, Knobloch, Alonso and Mercader2006; Mercader et al. Reference Mercader, Batiste, Alonso and Knobloch2013) and transition to turbulence (Pringle, Willis & Kerswell Reference Pringle, Willis and Kerswell2015) – see also Knobloch (Reference Knobloch2008, Reference Knobloch2015), Dawes (Reference Dawes2010) and Descalzi et al. (Reference Descalzi, Clerc, Residori and Assanto2011) for broader reviews. In the homoclinic snaking scenario (Pomeau Reference Pomeau1986; Woods & Champneys Reference Woods and Champneys1999; Coullet, Riera & Tresser Reference Coullet, Riera and Tresser2000), each alternating turn of a ‘snake’ in control parameter phase space is correlated with the emergence of a further interior cell of the localised pattern. This scenario has proven to be an important mechanism for localisation in more than a hundred theoretical studies. However, experimental evidence is limited, so far, to buckling (Thompson Reference Thompson2015), a semiconductor laser (Barbay et al. Reference Barbay, Hachair, Elsass, Sagnes and Kuszelewicz2008), vertically vibrated media (Umbanhowar, Melo & Swinney Reference Umbanhowar, Melo and Swinney1996), nonlinear optics (Akhmediev & Ankiewicz Reference Akhmediev and Ankiewicz2005), gas discharges (Purwins, Bödeker & Amiranashvili Reference Purwins, Bödeker and Amiranashvili2010), a light valve (Haudin et al. Reference Haudin, Rojas, Bortolozzo, Residori and Clerc2011) and, in the context of fluids, the Taylor–Couette flow (Abshagen et al. Reference Abshagen, Heise, Pfister and Mullin2010; Schneider et al. Reference Schneider, Gibson and Burke2010). A pending problem is a comparison of experiment and theory of homoclinic snaking for fully localised two-dimensional (2D) patterns (not just structures that are localised in a single spatial direction) in a physical fluid system.
A step towards filling this gap is investigating the surface instability of an electrically or magnetically polarisable fluid, because spatial inhomogeneities and noise are very low. When a static layer of magnetic fluid is subjected to a vertical magnetic field, it becomes unstable when a critical value
![]() $B_{c}$
of the magnetic induction is surpassed. Owing to this Rosensweig instability (Cowley & Rosensweig Reference Cowley and Rosensweig1967), a regular hexagonal pattern of cellular spikes emerges. By applying local magnetic pulses, localised radially symmetric spikes could be generated on the free-surface (Richter & Barashenkov Reference Richter and Barashenkov2005). In this paper we demonstrate that various localised hexagon patches as in figure 1 emerge spontaneously if the homogeneous field is switched into a regime where we expect to find homoclinic snaking. So far, the modelling of localised spikes is limited to finite element simulations (Lavrova, Matthies & Tobiska Reference Lavrova, Matthies and Tobiska2008; Cao & Ding Reference Cao and Ding2014) and a simple reaction–diffusion model (Richter & Barashenkov Reference Richter and Barashenkov2005). However, the Rosensweig instability involves a free-surface and so the justification of reaction–diffusion theory is problematic. Solving the full dynamic equations, we present numerical evidence that the localised hexagon patches undergo homoclinic snaking similar to that observed in reaction–diffusion theory (Woods & Champneys Reference Woods and Champneys1999; Coullet et al.
Reference Coullet, Riera and Tresser2000).
$B_{c}$
of the magnetic induction is surpassed. Owing to this Rosensweig instability (Cowley & Rosensweig Reference Cowley and Rosensweig1967), a regular hexagonal pattern of cellular spikes emerges. By applying local magnetic pulses, localised radially symmetric spikes could be generated on the free-surface (Richter & Barashenkov Reference Richter and Barashenkov2005). In this paper we demonstrate that various localised hexagon patches as in figure 1 emerge spontaneously if the homogeneous field is switched into a regime where we expect to find homoclinic snaking. So far, the modelling of localised spikes is limited to finite element simulations (Lavrova, Matthies & Tobiska Reference Lavrova, Matthies and Tobiska2008; Cao & Ding Reference Cao and Ding2014) and a simple reaction–diffusion model (Richter & Barashenkov Reference Richter and Barashenkov2005). However, the Rosensweig instability involves a free-surface and so the justification of reaction–diffusion theory is problematic. Solving the full dynamic equations, we present numerical evidence that the localised hexagon patches undergo homoclinic snaking similar to that observed in reaction–diffusion theory (Woods & Champneys Reference Woods and Champneys1999; Coullet et al.
Reference Coullet, Riera and Tresser2000).

Figure 1. A patch of seven ferrofluidic spikes seen together with the upper coil (a), and zoom in the high density range (b). Photographs courtesy of Robin Maretzki (a) and Achim Beetz (b).
The outline of the article is as follows. In § 2, we describe the experimental set-up, which is followed by a characterisation of the ferrofluid (§ 3) and the experimental results (§ 4). In § 5 we then introduce the mathematical model for the experiment, which we numerically solve in § 6 and present the numerical results. Then § 7 compares experimental and theoretical results. We finish with conclusions and outlook (§ 8).
2. Experimental set-up
Our experimental set-up is sketched in figure 2(a). An X-ray point source emits radiation vertically from above through the container with the ferrofluid, which is placed midway between a Helmholtz pair of coils. Underneath the container, an X-ray camera records the radiation passing through the layer of ferrofluid. The intensity at each pixel of the detector is directly related to the height of the fluid above that pixel. Therefore, the full surface topography can be reconstructed after calibration (Richter & Bläsing Reference Richter and Bläsing2001; Gollwitzer et al. Reference Gollwitzer, Matthies, Richter, Rehberg and Tobiska2007).

Figure 2. Set-up of the apparatus for measuring the Rosensweig instability. Scheme of the assembled set-up (a), and exploded view of the container with the coils (b).
The container, which holds the ferrofluid sample, is depicted in figure 2(b). It is a regular octagon machined from aluminium with a side length of 77 mm and two concentric inner bores with a diameter of 140 mm. These circular holes are carved from above and below, leaving only a thin base in the middle of the vessel with a thickness of 2 mm. On top of the octagon, a circular lid of aluminium is placed, which closes the hole from above (see figure 2
b). Each side of the octagon is equipped with a thermoelectric element QC-127-1.4-8.5MS from Quick-Ohm. These are powered by a 1.2 kW Kepco KLP-20-120 power supply. The hot side of the thermoelectric elements is connected to water-cooled heat exchangers. The temperature is measured at the bottom of the aluminium container with a Pt100 resistor. The temperature difference between the centre and the edge of the bottom plate does not exceed 0.1 K at temperature
![]() $10.0\,^{\circ }\text{C}$
measured at the edge of the vessel. A closed loop control, realised using a computer and programmable interface devices, holds the temperature
$10.0\,^{\circ }\text{C}$
measured at the edge of the vessel. A closed loop control, realised using a computer and programmable interface devices, holds the temperature
![]() ${\it\theta}$
of the vessel constant with an accuracy of 10 mK.
${\it\theta}$
of the vessel constant with an accuracy of 10 mK.
The container is surrounded by a Helmholtz pair of coils, thermally isolated from the vessel with a ring made from a flame-resistant composite material (FR-2). As shown in figure 2, the diameter of the coils is intentionally smaller than the diameter of the vessel in order to introduce a magnetic ramp. With this arrangement, the magnetic field strength falls off towards the border of the vessel, where it reaches 80 % of its value in the centre. The ramp is introduced in order to minimise the differences between the amplitudes obtained in a finite and an infinite geometry. For details of the magnetic ramp, see Knieling, Rehberg & Richter (Reference Knieling, Rehberg and Richter2010). Filling the container to a height of 5 mm with ferrofluid enhances the magnetic induction in comparison with the empty coils for the same current
![]() $I$
. Therefore
$I$
. Therefore
![]() $B(I)$
is measured immediately beneath the bottom of the container, at the central position, and serves as the control parameter in the following.
$B(I)$
is measured immediately beneath the bottom of the container, at the central position, and serves as the control parameter in the following.
3. Properties of the magnetic fluid
For the experiments, we use the ferrofluid APG E32 from Ferrotec Co. Table 1 lists the important material parameters. The density
![]() ${\it\rho}$
was measured utilising an electronic density meter (DMA 4100) from Anton Paar. The surface tension was measured by means of a ring tensiometer (Lauda TE 1) and corroborated by the pendant drop mehode (Dataphysics OCA 20).
${\it\rho}$
was measured utilising an electronic density meter (DMA 4100) from Anton Paar. The surface tension was measured by means of a ring tensiometer (Lauda TE 1) and corroborated by the pendant drop mehode (Dataphysics OCA 20).
Table 1. Properties of the magnetic fluid APG E32 (Lot G090707A) from Ferrotec Co.

The viscosity
![]() ${\it\eta}$
has been measured in the temperature range of
${\it\eta}$
has been measured in the temperature range of
![]() $-5\,^{\circ }\text{C}\leqslant {\it\theta}\leqslant 20\,^{\circ }\text{C}$
, using a commercial rheometer (MCR 301, Anton Paar) with a shear cell featuring a cone–plate geometry. At room temperature, the magnetic fluid with a viscosity of
$-5\,^{\circ }\text{C}\leqslant {\it\theta}\leqslant 20\,^{\circ }\text{C}$
, using a commercial rheometer (MCR 301, Anton Paar) with a shear cell featuring a cone–plate geometry. At room temperature, the magnetic fluid with a viscosity of
![]() ${\it\eta}=2~\text{Pa}~\text{s}$
is 2000 times more viscous than water. The value of
${\it\eta}=2~\text{Pa}~\text{s}$
is 2000 times more viscous than water. The value of
![]() ${\it\eta}$
can be increased by a factor of 9 when the liquid is cooled to
${\it\eta}$
can be increased by a factor of 9 when the liquid is cooled to
![]() $-5\,^{\circ }\text{C}$
. The temperature-dependent viscosity data can be well described by the Vogel–Fulcher law (Rault Reference Rault2000)
$-5\,^{\circ }\text{C}$
. The temperature-dependent viscosity data can be well described by the Vogel–Fulcher law (Rault Reference Rault2000)
with
![]() ${\it\eta}_{0}=0.48~\text{mPa}~\text{s}$
,
${\it\eta}_{0}=0.48~\text{mPa}~\text{s}$
,
![]() ${\it\psi}=1074~\text{K}$
and
${\it\psi}=1074~\text{K}$
and
![]() ${\it\theta}_{0}=-107.5\,^{\circ }\text{C}$
, as reported in detail by Gollwitzer, Rehberg & Richter (Reference Gollwitzer, Rehberg and Richter2010). For the present measurements, we chose a temperature of
${\it\theta}_{0}=-107.5\,^{\circ }\text{C}$
, as reported in detail by Gollwitzer, Rehberg & Richter (Reference Gollwitzer, Rehberg and Richter2010). For the present measurements, we chose a temperature of
![]() ${\it\theta}=10\,^{\circ }\text{C}$
, where the viscosity amounts to
${\it\theta}=10\,^{\circ }\text{C}$
, where the viscosity amounts to
![]() ${\it\eta}=4.48~\text{Pa}~\text{s}$
according to (3.1).
${\it\eta}=4.48~\text{Pa}~\text{s}$
according to (3.1).
The magnetisation,
![]() $\boldsymbol{M}(\boldsymbol{H}_{F})$
, where
$\boldsymbol{M}(\boldsymbol{H}_{F})$
, where
![]() $\boldsymbol{H}_{F}$
is the magnetic field in the fluid, has been measured by means of a fluxmetric magnetometer (Lakeshore Model 480). A spherical cavity with a volume of 1 ml was constructed from Perspex and filled up to the brim with the magnetic fluid. By means of X-rays we checked for a bubble-free filling. Figure 3(a) presents the measured data together with a fit (solid line) by the equation
$\boldsymbol{H}_{F}$
is the magnetic field in the fluid, has been measured by means of a fluxmetric magnetometer (Lakeshore Model 480). A spherical cavity with a volume of 1 ml was constructed from Perspex and filled up to the brim with the magnetic fluid. By means of X-rays we checked for a bubble-free filling. Figure 3(a) presents the measured data together with a fit (solid line) by the equation
 $$\begin{eqnarray}M(H_{\mathit{F}})=M_{\mathit{S}}\frac{H_{\mathit{F}}}{H_{\mathit{F}}+{\displaystyle \frac{M_{\mathit{S}}}{{\it\mu}_{\mathit{r},i}-1}}},\end{eqnarray}$$
$$\begin{eqnarray}M(H_{\mathit{F}})=M_{\mathit{S}}\frac{H_{\mathit{F}}}{H_{\mathit{F}}+{\displaystyle \frac{M_{\mathit{S}}}{{\it\mu}_{\mathit{r},i}-1}}},\end{eqnarray}$$
utilised by Fröhlich (Reference Fröhlich1881) and Vislovich (Reference Vislovich1990), where
![]() $M=|\boldsymbol{M}|$
,
$M=|\boldsymbol{M}|$
,
![]() $M_{\mathit{S}}$
is the saturation magnetisation,
$M_{\mathit{S}}$
is the saturation magnetisation,
![]() $H_{\mathit{F}}$
is the magnitude of the applied magnetic field in the fluid and
$H_{\mathit{F}}$
is the magnitude of the applied magnetic field in the fluid and
![]() ${\it\mu}_{\mathit{r},i}$
is the initial magnetic permeability.
${\it\mu}_{\mathit{r},i}$
is the initial magnetic permeability.
Fitting the data with (3.2) we obtain for the initial magnetic permeability
![]() ${\it\mu}_{\mathit{r},i}=4.57$
, and for the saturation magnetisation
${\it\mu}_{\mathit{r},i}=4.57$
, and for the saturation magnetisation
![]() $M_{\mathit{S}}=23.15~\text{kA}~\text{m}^{-1}$
. Equation (3.2) is used to calculate the chord permeability
$M_{\mathit{S}}=23.15~\text{kA}~\text{m}^{-1}$
. Equation (3.2) is used to calculate the chord permeability
and the tangent permeability
 $$\begin{eqnarray}{\it\mu}_{\mathit{ta}}\equiv \frac{\partial M}{\partial H_{\mathit{F}}}+1=\frac{{\it\mu}_{\mathit{r},i}-1}{\left(1+({\it\mu}_{\mathit{r},i}-1)\displaystyle \frac{H_{\mathit{F}}}{M_{\mathit{S}}}\right)^{2}}+1,\end{eqnarray}$$
$$\begin{eqnarray}{\it\mu}_{\mathit{ta}}\equiv \frac{\partial M}{\partial H_{\mathit{F}}}+1=\frac{{\it\mu}_{\mathit{r},i}-1}{\left(1+({\it\mu}_{\mathit{r},i}-1)\displaystyle \frac{H_{\mathit{F}}}{M_{\mathit{S}}}\right)^{2}}+1,\end{eqnarray}$$
which are displayed in figure 3(b) by a dashed red (blue) line, respectively. The effective permeability
is the geometric mean of the two permeabilities (Cowley & Rosensweig Reference Cowley and Rosensweig1967) and is marked in figure 3(b) by the black solid line.

Figure 3. (a) Measured magnetisation,
![]() $M$
, curve versus the field in the fluid,
$M$
, curve versus the field in the fluid,
![]() $H_{F}$
, and (b) related chord (red dashed), tangent (blue dashed) and effective (black solid line) permeabilities. The dotted line marks
$H_{F}$
, and (b) related chord (red dashed), tangent (blue dashed) and effective (black solid line) permeabilities. The dotted line marks
![]() ${\it\mu}_{\mathit{eff}}$
at
${\it\mu}_{\mathit{eff}}$
at
![]() $H_{c}$
.
$H_{c}$
.
By means of
![]() ${\it\mu}_{\mathit{eff}}(M)$
, the material parameters
${\it\mu}_{\mathit{eff}}(M)$
, the material parameters
![]() ${\it\sigma}$
and
${\it\sigma}$
and
![]() ${\it\rho}$
, and the gravitational acceleration
${\it\rho}$
, and the gravitational acceleration
![]() $g=9.81~\text{m}~\text{s}^{-2}$
, the critical magnetisation for a semi-infinite layer of ferrofluid is approximated by the implicit equation (Rosensweig Reference Rosensweig1985)
$g=9.81~\text{m}~\text{s}^{-2}$
, the critical magnetisation for a semi-infinite layer of ferrofluid is approximated by the implicit equation (Rosensweig Reference Rosensweig1985)
By numerically solving the implicit equation, we obtain
![]() $M_{\text{c}}=6.2303~\text{kA}~\text{m}^{-1}$
,
$M_{\text{c}}=6.2303~\text{kA}~\text{m}^{-1}$
,
![]() $H_{\text{c}}=2.3872~\text{kA}~\text{m}^{-1}$
and
$H_{\text{c}}=2.3872~\text{kA}~\text{m}^{-1}$
and
![]() $B_{\text{c}}={\it\mu}_{0}(H_{\text{c}}+M_{\text{c}})=10.83~\text{mT}$
. Note that this value is just an approximation for a semi-infinite layer of ferrofluid. Revisiting figure 3(b), we see that
$B_{\text{c}}={\it\mu}_{0}(H_{\text{c}}+M_{\text{c}})=10.83~\text{mT}$
. Note that this value is just an approximation for a semi-infinite layer of ferrofluid. Revisiting figure 3(b), we see that
![]() ${\it\mu}_{\mathit{eff}}$
drops considerably for increasing field. At the critical field, we find
${\it\mu}_{\mathit{eff}}$
drops considerably for increasing field. At the critical field, we find
![]() ${\it\mu}_{\mathit{eff}}(H_{c})=3.2$
(cf. the dotted line). The critical induction found by fitting amplitude equations to the experimental data (Gollwitzer et al.
Reference Gollwitzer, Rehberg and Richter2010) is about 4 % higher (cf. table 1).
${\it\mu}_{\mathit{eff}}(H_{c})=3.2$
(cf. the dotted line). The critical induction found by fitting amplitude equations to the experimental data (Gollwitzer et al.
Reference Gollwitzer, Rehberg and Richter2010) is about 4 % higher (cf. table 1).

Figure 4. (a) The bifurcation diagram (black line) of this pattern is obtained by fitting equation (11) in Gollwitzer et al. (Reference Gollwitzer, Rehberg and Richter2010) to about 170 000 measured data. Via the path indicated by the arrows, one obtains localised patches, as shown in (c). The magnetic induction
![]() $B$
is kept fixed during (1) for a time delay of
$B$
is kept fixed during (1) for a time delay of
![]() ${\it\tau}_{1}$
, then
${\it\tau}_{1}$
, then
![]() $B$
is switched to (2) for a time delay of
$B$
is switched to (2) for a time delay of
![]() ${\it\tau}_{2}$
before finally being switched to (3) until equilibrium is reached at point (3b). (b) A reconstruction of the height field of the domain-covering hexagons at point (1b). (c) Gives a reconstruction of the height field of a three-spike patch at point (3b) in the bifurcation diagram.
${\it\tau}_{2}$
before finally being switched to (3) until equilibrium is reached at point (3b). (b) A reconstruction of the height field of the domain-covering hexagons at point (1b). (c) Gives a reconstruction of the height field of a three-spike patch at point (3b) in the bifurcation diagram.
We stress that the mapping between a linear and a nonlinear
![]() $M(H)$
by (3.5) is only valid in the linear regime of pattern formation, i.e. for the onset of the instability, but not for the fully developed nonlinear patterns.
$M(H)$
by (3.5) is only valid in the linear regime of pattern formation, i.e. for the onset of the instability, but not for the fully developed nonlinear patterns.
4. Experimental results
In the investigated regime, the plain surface and domain-covering regular up-hexagonal (i.e. hexagons whose maximum amplitude is positive) patterns are bistable (
![]() $10.95~\text{mT}\leqslant B\leqslant 11.23~\text{mT}$
), as shown by the bifurcation diagram in figure 4(a), which stems from a fit to about 170 000 measured data points (Gollwitzer et al.
Reference Gollwitzer, Rehberg and Richter2010). Figure 4(b) displays an experimental realisation of the domain-covering hexagonal pattern observed at the upper branch, the infinite extension of which has the symmetry of the dihedral group
$10.95~\text{mT}\leqslant B\leqslant 11.23~\text{mT}$
), as shown by the bifurcation diagram in figure 4(a), which stems from a fit to about 170 000 measured data points (Gollwitzer et al.
Reference Gollwitzer, Rehberg and Richter2010). Figure 4(b) displays an experimental realisation of the domain-covering hexagonal pattern observed at the upper branch, the infinite extension of which has the symmetry of the dihedral group
![]() $\mathbb{D}_{6}$
.
$\mathbb{D}_{6}$
.
Owing to the high viscosity of the magnetic fluid, the formation of Rosensweig patterns takes 60 s. This allows us to vary the magnetic induction
![]() $B$
(the control parameter) and the pattern amplitude
$B$
(the control parameter) and the pattern amplitude
![]() $A$
almost independently. In this way we can enter the region around the unstable branch of the instability, where homoclinic snaking is suspected, from the side, as sketched in figure 4.
$A$
almost independently. In this way we can enter the region around the unstable branch of the instability, where homoclinic snaking is suspected, from the side, as sketched in figure 4.
Starting from a flat layer,
![]() $B$
is always switched to an overcritical value
$B$
is always switched to an overcritical value
![]() $B_{1}=11.45~\text{mT}$
, cf. position (1a) in figure 4. With time, the amplitude of the domain-covering hexagon pattern increases along path (1). After
$B_{1}=11.45~\text{mT}$
, cf. position (1a) in figure 4. With time, the amplitude of the domain-covering hexagon pattern increases along path (1). After
![]() ${\it\tau}_{1}=60.0~\text{s}$
this pattern is stabilised (1b). Then
${\it\tau}_{1}=60.0~\text{s}$
this pattern is stabilised (1b). Then
![]() $B$
is switched to a value
$B$
is switched to a value
![]() $B_{2}=10.74~\text{mT}$
before the fold of the hexagons and the magnetic fluid is allowed to relax from (2a) towards the flat state. Before the magnetic fluid flattens completely,
$B_{2}=10.74~\text{mT}$
before the fold of the hexagons and the magnetic fluid is allowed to relax from (2a) towards the flat state. Before the magnetic fluid flattens completely,
![]() $B$
is switched at (2b) to a value
$B$
is switched at (2b) to a value
![]() $B_{3}$
in the neighbourhood (3a) of the unstable branch of the imperfect transcritical bifurcation (cf. equations (1) and (2) in Gollwitzer et al.
Reference Gollwitzer, Rehberg and Richter2010), marked by a dashed line and shaded region in figure 4. Now the pattern relaxes on path (3a) to (3b), where the height of the patch finally settles down (equilibrates) to a value approximately 1.5 mm higher (depending on the size of the patch, i.e. for larger patches, the height tends to that for the domain-covering hexagons) than the domain-covering hexagons. A movie (available at http://dx.doi.org/10.1017/jfm.2015.565) shows the birth of a three-spike patch. Each patch was at least stable for 120 s, as recorded by the measuring programme. Moreover, we have checked the long-term stability of exemplary patches after generation and observed no decay for more than 2 h.
$B_{3}$
in the neighbourhood (3a) of the unstable branch of the imperfect transcritical bifurcation (cf. equations (1) and (2) in Gollwitzer et al.
Reference Gollwitzer, Rehberg and Richter2010), marked by a dashed line and shaded region in figure 4. Now the pattern relaxes on path (3a) to (3b), where the height of the patch finally settles down (equilibrates) to a value approximately 1.5 mm higher (depending on the size of the patch, i.e. for larger patches, the height tends to that for the domain-covering hexagons) than the domain-covering hexagons. A movie (available at http://dx.doi.org/10.1017/jfm.2015.565) shows the birth of a three-spike patch. Each patch was at least stable for 120 s, as recorded by the measuring programme. Moreover, we have checked the long-term stability of exemplary patches after generation and observed no decay for more than 2 h.
Starting at the edge of the bistable region defined by the fold of the domain-covering cellular hexagon spikes and increasing
![]() $B_{3}$
, we obtain a sequence of localised states ranging from solitary spikes to patches containing multiple spikes/hexagon cells on an otherwise flat fluid surface with two to 24 cells, as shown in figure 5 for
$B_{3}$
, we obtain a sequence of localised states ranging from solitary spikes to patches containing multiple spikes/hexagon cells on an otherwise flat fluid surface with two to 24 cells, as shown in figure 5 for
![]() ${\it\tau}_{2}=10.0~\text{s}$
. The height of the spikes/cells of a patch are not uniform; we observe that spikes near the centre of the patch are higher than those on the edge of the patch. The distance between spikes within a patch is approximately the same as the spatial period of the domain-covering hexagon pattern. Remarkably, the spikes do not spread out in space as time increases despite their magnetic dipole–dipole repulsion, originating from the fact that the spikes are magnetised in parallel. In this way the patches are not an ensemble of weakly interacting solitary spikes in the sense of Richter & Barashenkov (Reference Richter and Barashenkov2005).
${\it\tau}_{2}=10.0~\text{s}$
. The height of the spikes/cells of a patch are not uniform; we observe that spikes near the centre of the patch are higher than those on the edge of the patch. The distance between spikes within a patch is approximately the same as the spatial period of the domain-covering hexagon pattern. Remarkably, the spikes do not spread out in space as time increases despite their magnetic dipole–dipole repulsion, originating from the fact that the spikes are magnetised in parallel. In this way the patches are not an ensemble of weakly interacting solitary spikes in the sense of Richter & Barashenkov (Reference Richter and Barashenkov2005).

Figure 5. Localised states for
![]() ${\it\tau}_{2}=10.0~\text{s}$
at (a)
${\it\tau}_{2}=10.0~\text{s}$
at (a)
![]() $B=11.0725~\text{mT}$
, (b)
$B=11.0725~\text{mT}$
, (b)
![]() $B=11.0857~\text{mT}$
, (c)
$B=11.0857~\text{mT}$
, (c)
![]() $B=11.1120~\text{mT}$
, (d)
$B=11.1120~\text{mT}$
, (d)
![]() $B=11.1648~\text{mT}$
, (e)
$B=11.1648~\text{mT}$
, (e)
![]() $B=11.1780~\text{mT}$
, (f)
$B=11.1780~\text{mT}$
, (f)
![]() $B=11.1911~\text{mT}$
, (g)
$B=11.1911~\text{mT}$
, (g)
![]() $B=11.2043~\text{mT}$
, (h)
$B=11.2043~\text{mT}$
, (h)
![]() $B=11.2175~\text{mT}$
and (i)
$B=11.2175~\text{mT}$
and (i)
![]() $B=11.2307~\text{mT}$
.
$B=11.2307~\text{mT}$
.

Figure 6. The number of spikes versus
![]() $B_{3}$
for different delays
$B_{3}$
for different delays
![]() ${\it\tau}_{2}=1.0~\text{s}$
(♢), 7.5 s (▵), 8.5 s (○), 9.5 s (▫) and 10.0 s (▿) exhibits plateaux. The plateaux at 3, 10, 12, 14 and 21 spikes, where patches are forming complete patches, are marked by horizontal lines.
${\it\tau}_{2}=1.0~\text{s}$
(♢), 7.5 s (▵), 8.5 s (○), 9.5 s (▫) and 10.0 s (▿) exhibits plateaux. The plateaux at 3, 10, 12, 14 and 21 spikes, where patches are forming complete patches, are marked by horizontal lines.
Moreover, it is interesting to note the mechanism by which hexagon cells are added to large patches as
![]() $B_{3}$
is increased. Going from figure 5(f) to (i), we see that spikes are added in the middle of the lower front in order to form a completed patch with dihedral symmetry
$B_{3}$
is increased. Going from figure 5(f) to (i), we see that spikes are added in the middle of the lower front in order to form a completed patch with dihedral symmetry
![]() $\mathbb{D}_{2}$
. It is also possible to see completed patches with
$\mathbb{D}_{2}$
. It is also possible to see completed patches with
![]() $\mathbb{D}_{6}$
symmetry, as shown in figure 1.
$\mathbb{D}_{6}$
symmetry, as shown in figure 1.
Similar patches have been uncovered in the 2D Swift–Hohenberg equation as a signature of homoclinic snaking (cf. Lloyd et al. Reference Lloyd, Sandstede, Avitabile and Champneys2008; Escaff & Descalzi Reference Escaff and Descalzi2009; Kozyreff & Chapman Reference Kozyreff and Chapman2013). Also the mechanisms governing the growth of a patch, as observed above, resemble the ones described by these authors.
As shown in figure 6, the number of spikes in a patch increases monotonically with
![]() $B_{3}$
, with clearly defined plateaux. The data related with figure 5 are marked by ▿ and have been recorded with a delay of
$B_{3}$
, with clearly defined plateaux. The data related with figure 5 are marked by ▿ and have been recorded with a delay of
![]() ${\it\tau}_{2}=10.0~\text{s}$
. Reducing
${\it\tau}_{2}=10.0~\text{s}$
. Reducing
![]() ${\it\tau}_{2}$
to 9.5 s (▫), 8.5 s (○) and 7.5 s (▵) shifts the curves to lower magnetic inductions: because the starting amplitudes are higher, a lower
${\it\tau}_{2}$
to 9.5 s (▫), 8.5 s (○) and 7.5 s (▵) shifts the curves to lower magnetic inductions: because the starting amplitudes are higher, a lower
![]() $B_{3}$
is sufficient to generate a localised patch. Most importantly the prominent plateaux at
$B_{3}$
is sufficient to generate a localised patch. Most importantly the prominent plateaux at
![]() $3,10,12,14,\ldots$
cells exist for all these values of
$3,10,12,14,\ldots$
cells exist for all these values of
![]() ${\it\tau}_{2}$
. For the very short delay of
${\it\tau}_{2}$
. For the very short delay of
![]() ${\it\tau}_{2}=1.0~\text{s}$
, the curve (♢) hardly exhibits plateaux (apart from the plateau at 27 spikes, which is the maximal size of a hexagonal pattern in the set-up). That is because, for
${\it\tau}_{2}=1.0~\text{s}$
, the curve (♢) hardly exhibits plateaux (apart from the plateau at 27 spikes, which is the maximal size of a hexagonal pattern in the set-up). That is because, for
![]() ${\it\tau}_{2}=1.0~\text{s}$
, the regular hexagonal pattern (see 1b in figure 4) has hardly decayed, and we cannot sensitively explore the phase space where homoclinic snaking occurs.
${\it\tau}_{2}=1.0~\text{s}$
, the regular hexagonal pattern (see 1b in figure 4) has hardly decayed, and we cannot sensitively explore the phase space where homoclinic snaking occurs.
5. Governing equations
In order to elucidate the snaking process, we numerically solve the full three-dimensional (3D) dynamical equations. The field in the fluid is modelled by Maxwell’s equations with no free currents and a Young–Laplace equation for the free-surface. Since there are no free currents, the magnetic field in the fluid,
![]() $\boldsymbol{H}_{F}$
, can be written in terms of a gradient field
$\boldsymbol{H}_{F}$
, can be written in terms of a gradient field
![]() $\boldsymbol{H}_{F}=h\hat{\boldsymbol{z}}-\boldsymbol{{\rm\nabla}}{\it\phi}$
, where
$\boldsymbol{H}_{F}=h\hat{\boldsymbol{z}}-\boldsymbol{{\rm\nabla}}{\it\phi}$
, where
![]() $h$
is the magnitude of the applied uniform magnetic field strength in the fluid in the vertical direction
$h$
is the magnitude of the applied uniform magnetic field strength in the fluid in the vertical direction
![]() $\hat{\boldsymbol{z}}$
and the non-uniform part of the field is described by
$\hat{\boldsymbol{z}}$
and the non-uniform part of the field is described by
![]() $-\boldsymbol{{\rm\nabla}}{\it\phi}$
. The magnetisation is given by the linear equation
$-\boldsymbol{{\rm\nabla}}{\it\phi}$
. The magnetisation is given by the linear equation
![]() $M(H_{F})=({\it\mu}_{r}-1)H_{\mathit{F}}$
, where
$M(H_{F})=({\it\mu}_{r}-1)H_{\mathit{F}}$
, where
![]() $H_{\mathit{F}}=|\boldsymbol{H}_{\mathit{F}}|$
and
$H_{\mathit{F}}=|\boldsymbol{H}_{\mathit{F}}|$
and
![]() ${\it\mu}_{r}=\text{const.}$
is the magnetic permeability of the magnetic fluid relative to that of free space,
${\it\mu}_{r}=\text{const.}$
is the magnetic permeability of the magnetic fluid relative to that of free space,
![]() ${\it\mu}_{0}$
. Thus the magnetic induction follows from the linear relation
${\it\mu}_{0}$
. Thus the magnetic induction follows from the linear relation
![]() $\boldsymbol{B}={\it\mu}_{r}{\it\mu}_{0}\boldsymbol{H}_{F}$
.
$\boldsymbol{B}={\it\mu}_{r}{\it\mu}_{0}\boldsymbol{H}_{F}$
.
Of course, a linear magnetisation law can only be a rough approximation of the real
![]() $M(H_{\mathit{F}})$
measured in the experiment (§ 3). Despite that, previous analytical studies, which are based on a linear
$M(H_{\mathit{F}})$
measured in the experiment (§ 3). Despite that, previous analytical studies, which are based on a linear
![]() $M(H_{\mathit{F}})$
, can successfully predict all regular planforms on the ferrofluids and their underlying bifurcations (see Gailitis Reference Gailitis1977; Friedrichs & Engel Reference Friedrichs and Engel2001; Friedrichs Reference Friedrichs2002; Bohlius, Brand & Pleiner Reference Bohlius, Brand and Pleiner2011). Likewise in our numerical study we aim to catch the decisive qualitative features seen in the experiment, and to elucidate whether they are connected to homoclinic snaking.
$M(H_{\mathit{F}})$
, can successfully predict all regular planforms on the ferrofluids and their underlying bifurcations (see Gailitis Reference Gailitis1977; Friedrichs & Engel Reference Friedrichs and Engel2001; Friedrichs Reference Friedrichs2002; Bohlius, Brand & Pleiner Reference Bohlius, Brand and Pleiner2011). Likewise in our numerical study we aim to catch the decisive qualitative features seen in the experiment, and to elucidate whether they are connected to homoclinic snaking.
The magnetic field in the air above the magnetic fluid is given by
![]() $\boldsymbol{H}_{A}={\it\mu}_{r}h\hat{\boldsymbol{z}}-\boldsymbol{{\rm\nabla}}{\it\chi}$
and the steady-state free-surface is given by
$\boldsymbol{H}_{A}={\it\mu}_{r}h\hat{\boldsymbol{z}}-\boldsymbol{{\rm\nabla}}{\it\chi}$
and the steady-state free-surface is given by
![]() $z={\it\zeta}(x,y)$
, with
$z={\it\zeta}(x,y)$
, with
![]() ${\it\zeta}=0$
corresponding to the flat state. The equations are non-dimensionalised using the critical wavenumber
${\it\zeta}=0$
corresponding to the flat state. The equations are non-dimensionalised using the critical wavenumber
![]() $k_{c}=\sqrt{{\it\rho}g/{\it\sigma}}$
for the length scale and
$k_{c}=\sqrt{{\it\rho}g/{\it\sigma}}$
for the length scale and
![]() $\sqrt{{\it\rho}g{\it\sigma}}$
for the unit of pressure, where
$\sqrt{{\it\rho}g{\it\sigma}}$
for the unit of pressure, where
![]() ${\it\rho}$
is the fluid density and
${\it\rho}$
is the fluid density and
![]() ${\it\sigma}$
is the surface tension. Furthermore, the amplitude
${\it\sigma}$
is the surface tension. Furthermore, the amplitude
![]() $h$
of the uniform field strength inside the magnetic fluid is rescaled using
$h$
of the uniform field strength inside the magnetic fluid is rescaled using
![]() ${\it\mu}_{r}$
,
${\it\mu}_{r}$
,
such that the instability occurs at
![]() $\mathscr{H}_{\mathit{c}}=1$
. We note that, when comparing (5.1) with the related equation (5.5) of Silber & Knobloch (Reference Silber and Knobloch1988), we have rescaled with respect to
$\mathscr{H}_{\mathit{c}}=1$
. We note that, when comparing (5.1) with the related equation (5.5) of Silber & Knobloch (Reference Silber and Knobloch1988), we have rescaled with respect to
![]() ${\it\mu}_{0}$
. The bifurcation parameter is then
${\it\mu}_{0}$
. The bifurcation parameter is then
We also note that
![]() ${\it\epsilon}$
depends on
${\it\epsilon}$
depends on
![]() ${\it\mu}_{r}$
. For a static magnetic fluid in a vertical field, the dimensionless equations are
${\it\mu}_{r}$
. For a static magnetic fluid in a vertical field, the dimensionless equations are
where
![]() $[\cdot ]_{-}^{+}$
is the value of the jump across the interface of the quantity in the brackets,
$[\cdot ]_{-}^{+}$
is the value of the jump across the interface of the quantity in the brackets,
![]() $\hat{\boldsymbol{n}}$
is the unit normal to the interface and
$\hat{\boldsymbol{n}}$
is the unit normal to the interface and
![]() ${\it\kappa}$
is the mean curvature of the surface (see Silber & Knobloch Reference Silber and Knobloch1988):
${\it\kappa}$
is the mean curvature of the surface (see Silber & Knobloch Reference Silber and Knobloch1988):
No-flux boundary conditions are imposed on the top and bottom of the domain, i.e.
![]() ${\it\phi}_{z}(\boldsymbol{x},-D)={\it\chi}_{z}(\boldsymbol{x},+D)=0$
where
${\it\phi}_{z}(\boldsymbol{x},-D)={\it\chi}_{z}(\boldsymbol{x},+D)=0$
where
![]() $\boldsymbol{x}=(x,y)$
. Solving (5.3a
) for the pressure, within a constant,
$\boldsymbol{x}=(x,y)$
. Solving (5.3a
) for the pressure, within a constant,
![]() $C$
, at the free-surface yields
$C$
, at the free-surface yields
The pressure can then be eliminated and the boundary conditions written in terms of the fields
![]() ${\it\zeta}(x,y),{\it\phi}(x,y,z)$
and
${\it\zeta}(x,y),{\it\phi}(x,y,z)$
and
![]() ${\it\chi}(x,y,z)$
, as well as two parameters,
${\it\chi}(x,y,z)$
, as well as two parameters,
![]() ${\it\mu}_{r}$
and
${\it\mu}_{r}$
and
![]() ${\it\epsilon}$
.
${\it\epsilon}$
.
The system of equations possesses a free energy given by
 $$\begin{eqnarray}\displaystyle {\mathcal{E}}({\it\zeta},{\it\phi},{\it\chi}) & = & \displaystyle \int _{{\it\Omega}}\left[\frac{1}{2}\left(\int _{{\it\zeta}(\boldsymbol{x})}^{D}|\boldsymbol{H}_{A}|^{2}\,\text{d}z+{\it\mu}_{r}\int _{-D}^{{\it\zeta}(\boldsymbol{x})}|\boldsymbol{H}_{F}|^{2}\,\text{d}z\right)-\frac{1}{2}{\it\zeta}^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,C{\it\zeta}+{\it\mu}_{r}h({\it\chi}_{z=D}-{\it\phi}_{z=-D})-\sqrt{1+|\boldsymbol{{\rm\nabla}}{\it\zeta}|^{2}}-1\vphantom{\int _{{\it\zeta}(\boldsymbol{x})}^{D}}\right]\,\text{d}\boldsymbol{x},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{E}}({\it\zeta},{\it\phi},{\it\chi}) & = & \displaystyle \int _{{\it\Omega}}\left[\frac{1}{2}\left(\int _{{\it\zeta}(\boldsymbol{x})}^{D}|\boldsymbol{H}_{A}|^{2}\,\text{d}z+{\it\mu}_{r}\int _{-D}^{{\it\zeta}(\boldsymbol{x})}|\boldsymbol{H}_{F}|^{2}\,\text{d}z\right)-\frac{1}{2}{\it\zeta}^{2}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,C{\it\zeta}+{\it\mu}_{r}h({\it\chi}_{z=D}-{\it\phi}_{z=-D})-\sqrt{1+|\boldsymbol{{\rm\nabla}}{\it\zeta}|^{2}}-1\vphantom{\int _{{\it\zeta}(\boldsymbol{x})}^{D}}\right]\,\text{d}\boldsymbol{x},\end{eqnarray}$$
made up of magnetic, hydrostatic and surface energies, respectively, with conservation of mass, with boundary conditions at the top and bottom of the domain, and with the boundary condition at the interface
![]() ${\it\phi}(\boldsymbol{x},{\it\zeta})-h{\it\zeta}(1-{\it\mu}_{r})={\it\chi}(\boldsymbol{x},{\it\zeta})$
as constraints, where
${\it\phi}(\boldsymbol{x},{\it\zeta})-h{\it\zeta}(1-{\it\mu}_{r})={\it\chi}(\boldsymbol{x},{\it\zeta})$
as constraints, where
![]() ${\it\Omega}\subset \mathbb{R}^{2}$
is the space domain of
${\it\Omega}\subset \mathbb{R}^{2}$
is the space domain of
![]() ${\it\zeta}(\boldsymbol{x})$
and
${\it\zeta}(\boldsymbol{x})$
and
![]() $\boldsymbol{x}=(x,y)$
. We note that Gailitis (Reference Gailitis1977) and Bohlius, Pleiner & Brand (Reference Bohlius, Pleiner and Brand2006) use other energy formulations without the boundary conditions and conservation of mass. The constant
$\boldsymbol{x}=(x,y)$
. We note that Gailitis (Reference Gailitis1977) and Bohlius, Pleiner & Brand (Reference Bohlius, Pleiner and Brand2006) use other energy formulations without the boundary conditions and conservation of mass. The constant
![]() $C$
is a Lagrange multiplier for the mass constraint:
$C$
is a Lagrange multiplier for the mass constraint:
![]() $\int _{{\it\Omega}}{\it\zeta}\,\text{d}\boldsymbol{x}$
equal to a constant. Taking variations of
$\int _{{\it\Omega}}{\it\zeta}\,\text{d}\boldsymbol{x}$
equal to a constant. Taking variations of
![]() ${\mathcal{E}}$
with respect to the free-surface
${\mathcal{E}}$
with respect to the free-surface
![]() ${\it\zeta}$
yields the interface equation (5.4a
), and taking variations with respect to
${\it\zeta}$
yields the interface equation (5.4a
), and taking variations with respect to
![]() ${\it\phi}$
and
${\it\phi}$
and
![]() ${\it\chi}$
, using the constraint, yields the Laplace equations (5.3b
) and (5.3c
) and the no-flux boundary conditions
${\it\chi}$
, using the constraint, yields the Laplace equations (5.3b
) and (5.3c
) and the no-flux boundary conditions
![]() ${\it\phi}_{z}(\boldsymbol{x},-D)={\it\chi}_{z}(\boldsymbol{x},+D)=0$
. The advantage of this free energy is that it represents the whole system and we can now numerically compute energies taking into account the magnetic fields.
${\it\phi}_{z}(\boldsymbol{x},-D)={\it\chi}_{z}(\boldsymbol{x},+D)=0$
. The advantage of this free energy is that it represents the whole system and we can now numerically compute energies taking into account the magnetic fields.
In order to fix the pressure constant,
![]() $C$
, we assume that the base state
$C$
, we assume that the base state
![]() $({\it\chi},{\it\phi},{\it\zeta})=(0,0,0)$
solves the equations corresponding to the mass constraint
$({\it\chi},{\it\phi},{\it\zeta})=(0,0,0)$
solves the equations corresponding to the mass constraint
![]() $\int _{{\it\Omega}}{\it\zeta}\,\text{d}\boldsymbol{x}=0$
. We choose to study the case of large depth of magnetic fluid and we set the depth,
$\int _{{\it\Omega}}{\it\zeta}\,\text{d}\boldsymbol{x}=0$
. We choose to study the case of large depth of magnetic fluid and we set the depth,
![]() $D$
, to be 10. For
$D$
, to be 10. For
![]() ${\it\mu}_{r}=2$
, this yields a depth of 16.42 mm, i.e. about three times the depth of the fluid in the experiment, which is sufficiently large that the domain-covering hexagons do not change as the depth is increased. We have ignored the effect of the shallow layer in our numerics since one would have to solve for an additional magnetic field below the magnetic fluid and apply suitable compatibility conditions.
${\it\mu}_{r}=2$
, this yields a depth of 16.42 mm, i.e. about three times the depth of the fluid in the experiment, which is sufficiently large that the domain-covering hexagons do not change as the depth is increased. We have ignored the effect of the shallow layer in our numerics since one would have to solve for an additional magnetic field below the magnetic fluid and apply suitable compatibility conditions.
Carrying out a coordinate transformation to flatten out the free-surface (Twombly & Thomas Reference Twombly and Thomas1983) given by
 $$\begin{eqnarray}\left(\begin{array}{@{}c@{}}x\\ y\\ z\end{array}\right)\rightarrow \left(\begin{array}{@{}c@{}}\hat{x}\\ {\hat{y}}\\ \hat{z}\end{array}\right)=\left(\begin{array}{@{}c@{}}x\\ y\\ \displaystyle \frac{z-{\it\zeta}}{D-{\it\zeta}}D\end{array}\right),\quad \text{for }{\it\zeta}<z<D,\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}x\\ y\\ z\end{array}\right)\rightarrow \left(\begin{array}{@{}c@{}}\hat{x}\\ {\hat{y}}\\ \hat{z}\end{array}\right)=\left(\begin{array}{@{}c@{}}x\\ y\\ \displaystyle \frac{z-{\it\zeta}}{D-{\it\zeta}}D\end{array}\right),\quad \text{for }{\it\zeta}<z<D,\end{eqnarray}$$
and
 $$\begin{eqnarray}\left(\begin{array}{@{}c@{}}x\\ y\\ z\end{array}\right)\rightarrow \left(\begin{array}{@{}c@{}}\hat{x}\\ {\hat{y}}\\ \hat{z}\end{array}\right)=\left(\begin{array}{@{}c@{}}x\\ y\\ \displaystyle \frac{z-{\it\zeta}}{D+{\it\zeta}}D\end{array}\right),\quad \text{for }-D<z<{\it\zeta},\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}c@{}}x\\ y\\ z\end{array}\right)\rightarrow \left(\begin{array}{@{}c@{}}\hat{x}\\ {\hat{y}}\\ \hat{z}\end{array}\right)=\left(\begin{array}{@{}c@{}}x\\ y\\ \displaystyle \frac{z-{\it\zeta}}{D+{\it\zeta}}D\end{array}\right),\quad \text{for }-D<z<{\it\zeta},\end{eqnarray}$$
we can perform a Legendre transformation in order to define a Hamiltonian. Arbitrarily taking the
![]() $x$
direction, we define the momenta coordinates
$x$
direction, we define the momenta coordinates
![]() ${\it\alpha}=\partial {\mathcal{E}}/\partial {\it\phi}_{x},{\it\beta}=\partial {\mathcal{E}}/\partial {\it\chi}_{x}$
and
${\it\alpha}=\partial {\mathcal{E}}/\partial {\it\phi}_{x},{\it\beta}=\partial {\mathcal{E}}/\partial {\it\chi}_{x}$
and
![]() ${\it\eta}=\partial {\mathcal{E}}/\partial {\it\zeta}_{x}$
. Then the Hamiltonian for the system is given by
${\it\eta}=\partial {\mathcal{E}}/\partial {\it\zeta}_{x}$
. Then the Hamiltonian for the system is given by
on the constraint manifold
![]() ${\mathcal{M}}=\{{\it\phi}(\boldsymbol{x},0)-h{\it\zeta}(1-{\it\mu}_{r})-{\it\chi}(\boldsymbol{x},0)=0,{\it\phi}_{x}(\boldsymbol{x},0)-h{\it\zeta}_{x}(1-{\it\mu}_{r})-{\it\chi}_{x}(\boldsymbol{x},0)=0\}$
; see Groves & Toland (Reference Groves and Toland1997) and Groves, Lloyd & Stylianou (Reference Groves, Lloyd and Stylianou2015) for the similar case of water waves.
${\mathcal{M}}=\{{\it\phi}(\boldsymbol{x},0)-h{\it\zeta}(1-{\it\mu}_{r})-{\it\chi}(\boldsymbol{x},0)=0,{\it\phi}_{x}(\boldsymbol{x},0)-h{\it\zeta}_{x}(1-{\it\mu}_{r})-{\it\chi}_{x}(\boldsymbol{x},0)=0\}$
; see Groves & Toland (Reference Groves and Toland1997) and Groves, Lloyd & Stylianou (Reference Groves, Lloyd and Stylianou2015) for the similar case of water waves.
The Hamiltonian (5.10) is a constant along solutions in the
![]() $x$
direction and provides a wavelength selection principle (see Lloyd et al. (Reference Lloyd, Sandstede, Avitabile and Champneys2008) for the same principle applied to the Swift–Hohenberg equation). In particular, if we evaluate
$x$
direction and provides a wavelength selection principle (see Lloyd et al. (Reference Lloyd, Sandstede, Avitabile and Champneys2008) for the same principle applied to the Swift–Hohenberg equation). In particular, if we evaluate
![]() ${\mathcal{H}}$
along any localised planar (hexagon) front connecting to the trivial state
${\mathcal{H}}$
along any localised planar (hexagon) front connecting to the trivial state
![]() ${\it\zeta}=0$
and the domain-covering hexagon pattern, we find that
${\it\zeta}=0$
and the domain-covering hexagon pattern, we find that
![]() ${\mathcal{H}}={\mathcal{H}}(\mathbf{0})$
along the limiting domain-covering hexagon pattern so that it belongs to the same level set. Generically,
${\mathcal{H}}={\mathcal{H}}(\mathbf{0})$
along the limiting domain-covering hexagon pattern so that it belongs to the same level set. Generically,
![]() ${\mathcal{H}}$
will only equal
${\mathcal{H}}$
will only equal
![]() ${\mathcal{H}}(\mathbf{0})$
at finitely many spatially periodic orbits in the family of spatially periodic patterns and will therefore serve as a selection principle that involves only the spatially periodic patterns; see Beck et al. (Reference Beck, Knobloch, Lloyd, Sandstede and Wagenknecht2009) for more details.
${\mathcal{H}}(\mathbf{0})$
at finitely many spatially periodic orbits in the family of spatially periodic patterns and will therefore serve as a selection principle that involves only the spatially periodic patterns; see Beck et al. (Reference Beck, Knobloch, Lloyd, Sandstede and Wagenknecht2009) for more details.
6. Numerical results
The 3D equations (5.3b,c
) and (5.4a
) are solved by first flattening out the free-surface using (5.8) and (5.9) so that the computational domains are fixed cuboids. We apply Neumann boundary conditions on the four sizes of
![]() ${\it\Omega}$
in order to remove the translational invariance in
${\it\Omega}$
in order to remove the translational invariance in
![]() $x$
and
$x$
and
![]() $y$
that would cause problems with Newton solvers. This choice of boundary conditions on
$y$
that would cause problems with Newton solvers. This choice of boundary conditions on
![]() ${\it\Omega}$
limits us to cellular hexagons, symmetric planar fronts and
${\it\Omega}$
limits us to cellular hexagons, symmetric planar fronts and
![]() $\mathbb{D}_{2}$
symmetric patches involving cellular hexagons computed on the positive quadrant; see Lloyd et al. (Reference Lloyd, Sandstede, Avitabile and Champneys2008) for more details. To remove the continuous symmetry due to the magnetic potentials being defined only up to a constant, we add an extra parameter
$\mathbb{D}_{2}$
symmetric patches involving cellular hexagons computed on the positive quadrant; see Lloyd et al. (Reference Lloyd, Sandstede, Avitabile and Champneys2008) for more details. To remove the continuous symmetry due to the magnetic potentials being defined only up to a constant, we add an extra parameter
![]() ${\it\lambda}$
to the Laplace equations (5.3b,c
) to be solved along with
${\it\lambda}$
to the Laplace equations (5.3b,c
) to be solved along with
![]() ${\it\phi},{\it\chi}$
and
${\it\phi},{\it\chi}$
and
![]() ${\it\zeta}$
and we append an extra equation (see Twombly & Thomas Reference Twombly and Thomas1983)
${\it\zeta}$
and we append an extra equation (see Twombly & Thomas Reference Twombly and Thomas1983)
We now have a well-posed boundary value problem with all the continuous symmetries removed, allowing us to use Newton methods. We discretise in MATLAB using fourth-order central finite differences (for planar fronts) or a pseudo-spectral Fourier method (for hexagon spikes and patches) in
![]() $x$
and
$x$
and
![]() $y$
directions and Chebyshev pseudo-spectral method in
$y$
directions and Chebyshev pseudo-spectral method in
![]() $z$
with a Newton–GMRES method (Kelley Reference Kelley2003) and secant pseudo-arclength continuation (Krauskopf, Osinga & Galan-Vioque Reference Krauskopf, Osinga and Galan-Vioque2007). For the Newton–GMRES scheme, one needs a preconditioner. For this we precompute a sparse incomplete LU-decomposition (with the Crout algorithm Saad (Reference Saad1996)) of the linear system with a flat interface at onset and this is fixed for the continuation. The incomplete LU-decomposition is computed with a drop tolerance of
$z$
with a Newton–GMRES method (Kelley Reference Kelley2003) and secant pseudo-arclength continuation (Krauskopf, Osinga & Galan-Vioque Reference Krauskopf, Osinga and Galan-Vioque2007). For the Newton–GMRES scheme, one needs a preconditioner. For this we precompute a sparse incomplete LU-decomposition (with the Crout algorithm Saad (Reference Saad1996)) of the linear system with a flat interface at onset and this is fixed for the continuation. The incomplete LU-decomposition is computed with a drop tolerance of
![]() $1\times 10^{-6}$
and we set a maximum of 20 iterations for GMRES with 40 Arnoldi restarts and a tolerance of
$1\times 10^{-6}$
and we set a maximum of 20 iterations for GMRES with 40 Arnoldi restarts and a tolerance of
![]() $10^{-4}$
. Typical spatial step sizes in
$10^{-4}$
. Typical spatial step sizes in
![]() $x$
and
$x$
and
![]() $y$
directions are 0.25–0.5 for the Fourier pseudo-spectral method and 20 Chebyshev collocation points in
$y$
directions are 0.25–0.5 for the Fourier pseudo-spectral method and 20 Chebyshev collocation points in
![]() $z$
and a fixed arclength step size of 0.01. The numerics are validated by comparing with normal-form results by Silber & Knobloch (Reference Silber and Knobloch1988). In particular, we check that the change of sub/supercriticality of rolls and squares occurs at the theoretically predicted values of
$z$
and a fixed arclength step size of 0.01. The numerics are validated by comparing with normal-form results by Silber & Knobloch (Reference Silber and Knobloch1988). In particular, we check that the change of sub/supercriticality of rolls and squares occurs at the theoretically predicted values of
![]() ${\it\mu}_{r}$
; see the appendix for more details. Fold loci are found by carrying out parameter slices and then doing a linear interpolation about the fold values. The Maxwell point is computed by appending the Hamiltonian and energy conditions to the system.
${\it\mu}_{r}$
; see the appendix for more details. Fold loci are found by carrying out parameter slices and then doing a linear interpolation about the fold values. The Maxwell point is computed by appending the Hamiltonian and energy conditions to the system.
In the following we present the results obtained with the procedures sketched above. We start with the hexagon Maxwell curve (§ 6.1), which is succeeded by hexagon planar fronts (§ 6.2), hexagon patches (§ 6.3) and rhomboid patches (§ 6.4).
6.1. Hexagon Maxwell curve
Intuitively, one expects localised patches to exist when the energy of a single hexagon cell of the infinitely extended pattern has the same energy as the trivial flat state. This occurs at the Maxwell point: a hexagon with a wavelength selected by
![]() ${\mathcal{H}}$
has the same energy
${\mathcal{H}}$
has the same energy
![]() ${\mathcal{E}}(\text{hex})={\mathcal{E}}(\mathbf{0})$
, where
${\mathcal{E}}(\text{hex})={\mathcal{E}}(\mathbf{0})$
, where
![]() $\text{hex}$
is a single hexagon cell. For
$\text{hex}$
is a single hexagon cell. For
![]() ${\it\mu}_{r}$
close to 1, the hexagon Maxwell point was previously computed analytically by Friedrichs & Engel (Reference Friedrichs and Engel2001) with an energy minimisation principle for the wavelength selection. In order to find a Maxwell curve relevant for localised hexagon patterns, one needs to use the Hamiltonian selection principle. We find that the Hamiltonian wavelength selection criterion only slightly changes the wavelength from that at onset. In figure 7, we trace out the hexagon Maxwell curve varying both
${\it\mu}_{r}$
close to 1, the hexagon Maxwell point was previously computed analytically by Friedrichs & Engel (Reference Friedrichs and Engel2001) with an energy minimisation principle for the wavelength selection. In order to find a Maxwell curve relevant for localised hexagon patterns, one needs to use the Hamiltonian selection principle. We find that the Hamiltonian wavelength selection criterion only slightly changes the wavelength from that at onset. In figure 7, we trace out the hexagon Maxwell curve varying both
![]() ${\it\epsilon}$
and
${\it\epsilon}$
and
![]() ${\it\mu}_{r}$
. We find that the Maxwell curve closely follows the fold of the domain-covering hexagons. In particular, for
${\it\mu}_{r}$
. We find that the Maxwell curve closely follows the fold of the domain-covering hexagons. In particular, for
![]() ${\it\mu}_{r}=2$
the Maxwell point is found to be
${\it\mu}_{r}=2$
the Maxwell point is found to be
![]() ${\it\epsilon}\approx -0.013$
. For
${\it\epsilon}\approx -0.013$
. For
![]() ${\it\mu}_{r}$
close to 1, the height of the hexagons becomes very small, making it difficult for our numerics to capture, since we only compute solutions to a relative error of
${\it\mu}_{r}$
close to 1, the height of the hexagons becomes very small, making it difficult for our numerics to capture, since we only compute solutions to a relative error of
![]() $10^{-4}$
and round-off error starts to dominate. We do believe, though, that the Maxwell curve should continue down to
$10^{-4}$
and round-off error starts to dominate. We do believe, though, that the Maxwell curve should continue down to
![]() ${\it\mu}_{r}=1$
.
${\it\mu}_{r}=1$
.

Figure 7. Two-parameter (
![]() ${\it\epsilon},{\it\mu}_{r}$
) bifurcation diagram showing the existence of the primary fold of the domain-covering hexagons and their corresponding Maxwell point.
${\it\epsilon},{\it\mu}_{r}$
) bifurcation diagram showing the existence of the primary fold of the domain-covering hexagons and their corresponding Maxwell point.
At the hexagon Maxwell curve, we expect to see stationary fronts between the flat state and domain-covering hexagons since we are connecting states with the same energy. Infinitely many different types of planar fronts are possible depending on the front’s interface with respect to the underlying hexagonal lattice. These different fronts can be classified by their Bravais–Miller index, which we denote by
![]() $\langle n_{1}n_{2}\rangle$
, where
$\langle n_{1}n_{2}\rangle$
, where
![]() $n_{j}$
are the reciprocals of the intercepts of the line with the lines
$n_{j}$
are the reciprocals of the intercepts of the line with the lines
![]() $\mathbb{R}\boldsymbol{l}_{i}$
generated by the lattice vectors
$\mathbb{R}\boldsymbol{l}_{i}$
generated by the lattice vectors
![]() $\boldsymbol{l}_{j}$
, assigning the reciprocal
$\boldsymbol{l}_{j}$
, assigning the reciprocal
![]() $n_{j}=0$
if the line does not intersect
$n_{j}=0$
if the line does not intersect
![]() $\mathbb{R}\boldsymbol{l}_{i}$
(see Ashcroft & Mermin Reference Ashcroft and Mermin1976; Lloyd et al.
Reference Lloyd, Sandstede, Avitabile and Champneys2008). It is these different types of fronts that form the sides of large hexagon patches.
$\mathbb{R}\boldsymbol{l}_{i}$
(see Ashcroft & Mermin Reference Ashcroft and Mermin1976; Lloyd et al.
Reference Lloyd, Sandstede, Avitabile and Champneys2008). It is these different types of fronts that form the sides of large hexagon patches.
6.2. Hexagon planar fronts
The works of Lloyd et al. (Reference Lloyd, Sandstede, Avitabile and Champneys2008), Escaff & Descalzi (Reference Escaff and Descalzi2009), Kozyreff & Chapman (Reference Kozyreff and Chapman2013) and Dean et al. (Reference Dean, Matthews, Cox and King2015) suggest that one needs only to consider two main hexagon planar fronts, namely the
![]() $\langle 10\rangle$
and
$\langle 10\rangle$
and
![]() $\langle 11\rangle$
fronts, in order to understand snaking of fully localised patches. We note that, in figure 5(f–i), we see that the patches are mostly made up of
$\langle 11\rangle$
fronts, in order to understand snaking of fully localised patches. We note that, in figure 5(f–i), we see that the patches are mostly made up of
![]() $\langle 10\rangle$
fronts, with figure 5(f) also showing the left- and right-hand sides that are
$\langle 10\rangle$
fronts, with figure 5(f) also showing the left- and right-hand sides that are
![]() $\langle 11\rangle$
fronts. Hence, we will concentrate on first understanding the
$\langle 11\rangle$
fronts. Hence, we will concentrate on first understanding the
![]() $\langle 10\rangle$
and
$\langle 10\rangle$
and
![]() $\langle 11\rangle$
hexagon planar fronts.
$\langle 11\rangle$
hexagon planar fronts.
Generically, we expect these hexagon fronts to remain pinned in an open region of parameter space, where they undergo homoclinic snaking about the Maxwell point (see Pomeau Reference Pomeau1986; Beck et al.
Reference Beck, Knobloch, Lloyd, Sandstede and Wagenknecht2009). This is confirmed by our numerical results presented in figure 8: for
![]() ${\it\mu}_{r}=2$
, indeed, the
${\it\mu}_{r}=2$
, indeed, the
![]() $\langle 10\rangle$
and
$\langle 10\rangle$
and
![]() $\langle 11\rangle$
fronts snake about the Maxwell point at
$\langle 11\rangle$
fronts snake about the Maxwell point at
![]() ${\it\epsilon}\approx -0.013$
. We find, similar to that reported in other systems (Lloyd et al.
Reference Lloyd, Sandstede, Avitabile and Champneys2008; Escaff & Descalzi Reference Escaff and Descalzi2009; Kozyreff & Chapman Reference Kozyreff and Chapman2013; Lloyd & O’Farrell Reference Lloyd and O’Farrell2013), that the
${\it\epsilon}\approx -0.013$
. We find, similar to that reported in other systems (Lloyd et al.
Reference Lloyd, Sandstede, Avitabile and Champneys2008; Escaff & Descalzi Reference Escaff and Descalzi2009; Kozyreff & Chapman Reference Kozyreff and Chapman2013; Lloyd & O’Farrell Reference Lloyd and O’Farrell2013), that the
![]() $\langle 10\rangle$
front snakes over a larger region of parameter space than the
$\langle 10\rangle$
front snakes over a larger region of parameter space than the
![]() $\langle 11\rangle$
front. This gives a partial explanation as to why mostly patches with
$\langle 11\rangle$
front. This gives a partial explanation as to why mostly patches with
![]() $\langle 10\rangle$
sides are observed in our experiments, as these live in a larger region of parameter space.
$\langle 10\rangle$
sides are observed in our experiments, as these live in a larger region of parameter space.
If the computational domain is commensurate with the domain-covering hexagons, then we expect the snaking branches to terminate near the fold of the domain-covering hexagons (see Dawes Reference Dawes2008). In figure 8, we have stopped the snaking branch early and indicate that the snaking should continue indefinitely for fronts on the plane.

Figure 8. The L2 norm of the displacement of the interface of localised planar hexagon fronts undergoes homoclinic snaking about the Maxwell point (▫) for
![]() ${\it\mu}_{r}=2$
. The
${\it\mu}_{r}=2$
. The
![]() $\langle 10\rangle$
front (blue) is snaking in a far larger region of parameter space than the
$\langle 10\rangle$
front (blue) is snaking in a far larger region of parameter space than the
![]() $\langle 11\rangle$
front (red). Here
$\langle 11\rangle$
front (red). Here
![]() $\Vert {\it\zeta}\Vert _{2}^{2}=(1/|{\it\Omega}|)\int _{{\it\Omega}}{\it\zeta}^{2}\,\text{d}\boldsymbol{x}$
is the normalised L2 norm of the interface.
$\Vert {\it\zeta}\Vert _{2}^{2}=(1/|{\it\Omega}|)\int _{{\it\Omega}}{\it\zeta}^{2}\,\text{d}\boldsymbol{x}$
is the normalised L2 norm of the interface.

Figure 9. Emergence of a fully localised hexagon patch (dashed purple) bifurcating from a single spike (green) with
![]() ${\it\mu}_{r}=2$
. We also plot the snaking regions of the
${\it\mu}_{r}=2$
. We also plot the snaking regions of the
![]() $\langle 10\rangle$
(blue) and
$\langle 10\rangle$
(blue) and
![]() $\langle 11\rangle$
planar fronts (red).
$\langle 11\rangle$
planar fronts (red).
6.3. Hexagon patches
We turn now from the planar fronts to the hexagonal patches as seen in the experiment. The numerical results for
![]() ${\it\mu}_{r}=2$
displayed in figure 9 show that radial spots bifurcate subcritically at onset from the flat state and undergo a subsequent fold. Along the upper branch of the spot there is a
${\it\mu}_{r}=2$
displayed in figure 9 show that radial spots bifurcate subcritically at onset from the flat state and undergo a subsequent fold. Along the upper branch of the spot there is a
![]() $\mathbb{D}_{6}$
bifurcation from which a hexagon patch emerges that undergoes a series of folds yielding larger and larger patches. We terminate the branch early, as the snaking branch becomes highly intricate further up the branch (cf. Lloyd et al. (Reference Lloyd, Sandstede, Avitabile and Champneys2008, figure 25)). However, we expect this branch to eventually terminate near the fold of the domain-covering hexagons. This patch also snakes about around the
$\mathbb{D}_{6}$
bifurcation from which a hexagon patch emerges that undergoes a series of folds yielding larger and larger patches. We terminate the branch early, as the snaking branch becomes highly intricate further up the branch (cf. Lloyd et al. (Reference Lloyd, Sandstede, Avitabile and Champneys2008, figure 25)). However, we expect this branch to eventually terminate near the fold of the domain-covering hexagons. This patch also snakes about around the
![]() $\langle 10\rangle$
and
$\langle 10\rangle$
and
![]() $\langle 11\rangle$
hexagon fronts (indicated by the shaded regions). We observe that the snaking occurs around the hexagon fronts since large patches are effectively made up of combinations of hexagon fronts’ sides. The hexagon patch displayed in the central inset of figure 9 occurs after the third fold of the hexagon patch branch, and comprises seven fully developed spikes together with an outer shell of 12 lower humps. It resembles the experimental patch presented in figure 1, which is also part of the
$\langle 11\rangle$
hexagon fronts (indicated by the shaded regions). We observe that the snaking occurs around the hexagon fronts since large patches are effectively made up of combinations of hexagon fronts’ sides. The hexagon patch displayed in the central inset of figure 9 occurs after the third fold of the hexagon patch branch, and comprises seven fully developed spikes together with an outer shell of 12 lower humps. It resembles the experimental patch presented in figure 1, which is also part of the
![]() ${\it\tau}_{2}=7.5~\text{s}$
series in figure 6.
${\it\tau}_{2}=7.5~\text{s}$
series in figure 6.
6.4. Rhomboid patches
As seen in the experimental patterns shown in figure 5, the localisation of the patches is not necessarily centred around a spike. The patches may equally well organise around a valley between two spikes. These structures have been called localised rhomboids (Lloyd et al.
Reference Lloyd, Sandstede, Avitabile and Champneys2008). As shown in figure 10, we are able to find these structures in the same parameter region as the localised hexagon patches. There are some crucial differences for these structures to the localised hexagon patches with a spike at the centre of the patch. The first difference is that rhomboid patches emerge not from a bifurcation of a single spike but from a double-spike configuration that bifurcates from the flat state. Figure 10 explains how patches are grown by first trying to complete a
![]() $\langle 10\rangle$
front side by first adding cells in the middle of each of these sides. As the patches get larger, we see the snaking becomes more confined to the
$\langle 10\rangle$
front side by first adding cells in the middle of each of these sides. As the patches get larger, we see the snaking becomes more confined to the
![]() $\langle 10\rangle$
and
$\langle 10\rangle$
and
![]() $\langle 11\rangle$
front snaking regions. In particular, when a patch has only
$\langle 11\rangle$
front snaking regions. In particular, when a patch has only
![]() $\langle 10\rangle$
front sides, then the snaking diagram makes its largest excursion by travelling from the leftmost
$\langle 10\rangle$
front sides, then the snaking diagram makes its largest excursion by travelling from the leftmost
![]() $\langle 11\rangle$
front limit to the rightmost
$\langle 11\rangle$
front limit to the rightmost
![]() $\langle 10\rangle$
. All other types of patches are confined to the
$\langle 10\rangle$
. All other types of patches are confined to the
![]() $\langle 11\rangle$
front region. We note that the existence regions of the various configurations are not the same.
$\langle 11\rangle$
front region. We note that the existence regions of the various configurations are not the same.

Figure 10. Emergence of fully localised rhomboid patches bifurcating from the flat state with
![]() ${\it\mu}_{r}=2$
. We also plot the snaking regions of the
${\it\mu}_{r}=2$
. We also plot the snaking regions of the
![]() $\langle 10\rangle$
(blue) and
$\langle 10\rangle$
(blue) and
![]() $\langle 11\rangle$
planar fronts (red).
$\langle 11\rangle$
planar fronts (red).
We shall briefly comment on the stability of the branch shown in figure 10. It is not possible to compute the stability of the branches directly from the numerics, since we have not written down an equation for the evolution of the fluid velocity. However, we expect the branch emanating from
![]() ${\it\epsilon}=0$
to initially be unstable since the bifurcation is subcritical. We anticipate that the branch then re-stabilises at the first fold to yield a stable two-spike patch and, between each subsequent fold, the branch will destabilise (due to an eigenvalue crossing the imaginary axis at the fold) and then re-stabilise (see Beck et al.
Reference Beck, Knobloch, Lloyd, Sandstede and Wagenknecht2009). Near each fold, we anticipate that there are symmetry-breaking bifurcations leading to non-
${\it\epsilon}=0$
to initially be unstable since the bifurcation is subcritical. We anticipate that the branch then re-stabilises at the first fold to yield a stable two-spike patch and, between each subsequent fold, the branch will destabilise (due to an eigenvalue crossing the imaginary axis at the fold) and then re-stabilise (see Beck et al.
Reference Beck, Knobloch, Lloyd, Sandstede and Wagenknecht2009). Near each fold, we anticipate that there are symmetry-breaking bifurcations leading to non-
![]() $\mathbb{D}_{2}$
symmetric patches.
$\mathbb{D}_{2}$
symmetric patches.
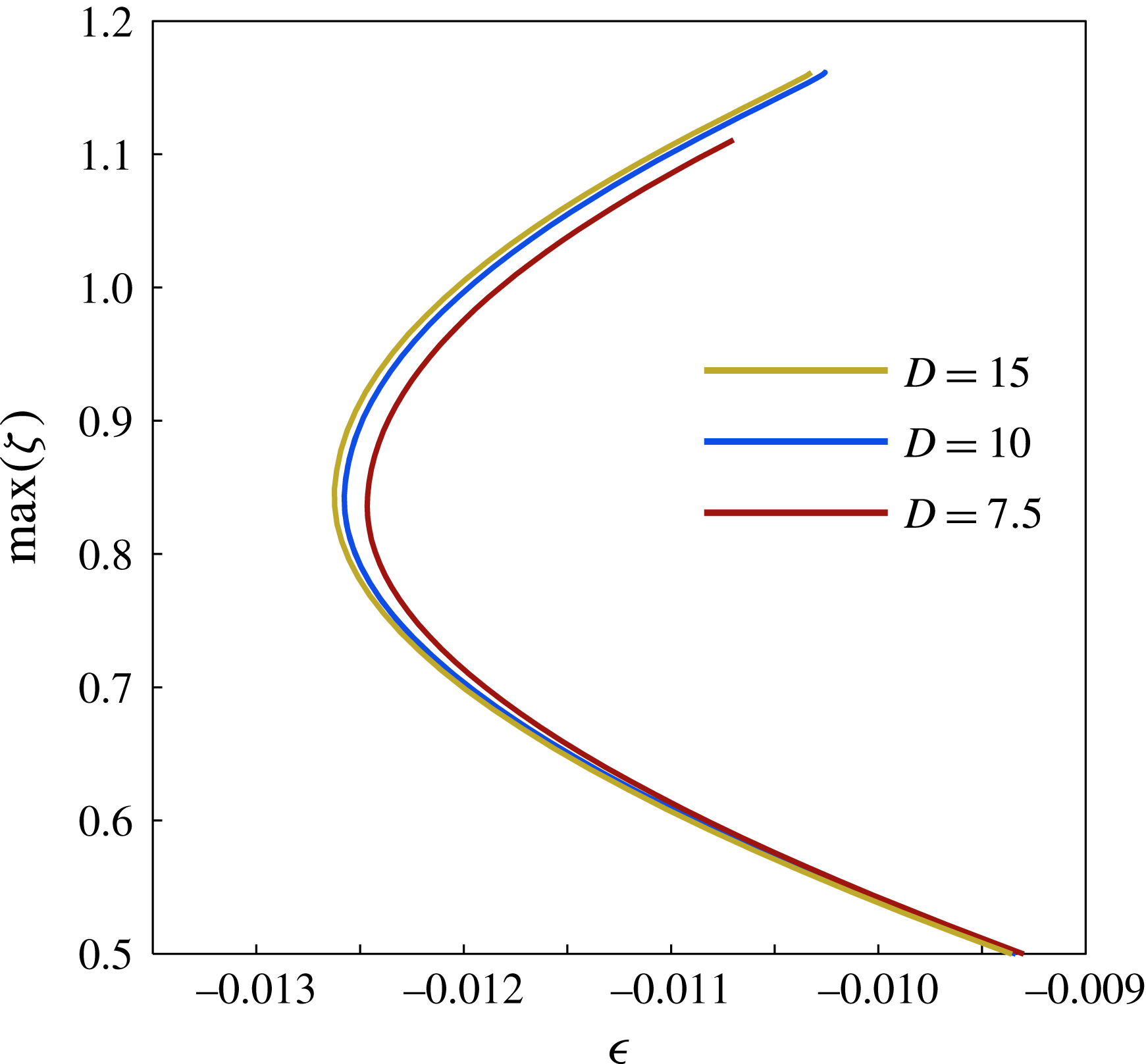
Figure 11. The height of the rhomboid patches for
![]() $D=7.5,10$
and 15 for
$D=7.5,10$
and 15 for
![]() ${\it\mu}_{r}=2$
up to the second fold. We observe that, as we decrease
${\it\mu}_{r}=2$
up to the second fold. We observe that, as we decrease
![]() $D$
, the height of the patches also decreases, but that for
$D$
, the height of the patches also decreases, but that for
![]() $D\geqslant 10$
we observe little change in the height.
$D\geqslant 10$
we observe little change in the height.
We eventually investigate the effect of changing the depth
![]() $D$
on the localised rhomboid patches. In figure 11, we plot the maximum height of the patches for
$D$
on the localised rhomboid patches. In figure 11, we plot the maximum height of the patches for
![]() $D=7.5,10$
and 15. For clarity we stop the bifurcation curves before the second fold. As the depth increases, the snaking diagrams are shifted to the left and the maximum height of the patches increases as well. It becomes clear that the existence regions of the localised patches are affected by the depth of the fluid. This is believed to be caused by the Neumann boundary conditions at the bottom (which insist that the magnetic field decays to the applied magnetic field here). In a shallow layer, that constraint also reduces the magnetic field within the tip of the spikes, and thus their maximum height.
$D=7.5,10$
and 15. For clarity we stop the bifurcation curves before the second fold. As the depth increases, the snaking diagrams are shifted to the left and the maximum height of the patches increases as well. It becomes clear that the existence regions of the localised patches are affected by the depth of the fluid. This is believed to be caused by the Neumann boundary conditions at the bottom (which insist that the magnetic field decays to the applied magnetic field here). In a shallow layer, that constraint also reduces the magnetic field within the tip of the spikes, and thus their maximum height.
7. Comparison between experimental and numerical results
We now turn to comparing our experimental and numerical results. As stated in § 5, our model is based on a linear magnetisation law, whereas we presented in § 3 the nonlinear
![]() $M(H_{\mathit{F}})$
of the real ferrofluid, with an effective permeability ranging from
$M(H_{\mathit{F}})$
of the real ferrofluid, with an effective permeability ranging from
![]() ${\it\mu}_{\mathit{eff}}=4.57$
at
${\it\mu}_{\mathit{eff}}=4.57$
at
![]() $B=0~\text{mT}$
down to 3.2 at
$B=0~\text{mT}$
down to 3.2 at
![]() $B_{c}=10.8~\text{mT}$
. Therefore, a direct matching of all experimental and numerical results cannot be expected. For
$B_{c}=10.8~\text{mT}$
. Therefore, a direct matching of all experimental and numerical results cannot be expected. For
![]() ${\it\mu}_{r}\rightarrow 1$
, the linear magnetisation law becomes a more accurate approximation of the nonlinear magnetisation law and the model predicts that homoclinic snaking should persist, albeit with an exponentially small width in which the snaking exists.
${\it\mu}_{r}\rightarrow 1$
, the linear magnetisation law becomes a more accurate approximation of the nonlinear magnetisation law and the model predicts that homoclinic snaking should persist, albeit with an exponentially small width in which the snaking exists.
In order to provide a comparison with the experimental results in § 4, we instead chose a magnetic permeability
![]() ${\it\mu}_{r}=\text{const.}$
for our model, which captures the qualitative features of the experiment. In a first attempt, we chose
${\it\mu}_{r}=\text{const.}$
for our model, which captures the qualitative features of the experiment. In a first attempt, we chose
![]() ${\it\mu}_{r}$
to be the effective permeability at the critical point
${\it\mu}_{r}$
to be the effective permeability at the critical point
![]() ${\it\mu}_{\mathit{eff}}(H_{c})=3.2$
(cf. figure 3
b) for the model:
${\it\mu}_{\mathit{eff}}(H_{c})=3.2$
(cf. figure 3
b) for the model:
![]() ${\it\mu}_{r}=3.2$
. In figure 12(a), we path-follow the two-spike patch, as depicted in figure 12(b), bifurcating from the flat state to the upper branch. As seen from figure 12(a), for
${\it\mu}_{r}=3.2$
. In figure 12(a), we path-follow the two-spike patch, as depicted in figure 12(b), bifurcating from the flat state to the upper branch. As seen from figure 12(a), for
![]() ${\it\mu}_{r}=3.2$
, localised structures exist from
${\it\mu}_{r}=3.2$
, localised structures exist from
![]() $B=10.3$
to 11.5 mT, which is a significantly larger range (about 200 %) than that observed in figure 6. Moreover, the height of the spikes is about 8 % larger than that observed experimentally.
$B=10.3$
to 11.5 mT, which is a significantly larger range (about 200 %) than that observed in figure 6. Moreover, the height of the spikes is about 8 % larger than that observed experimentally.

Figure 12. (a) Numerical bifurcation diagram for
![]() ${\it\mu}_{r}=3.2$
for a two-spike configuration, depicted in (b), that has bifurcated off the flat state. The state in (b) was computed for
${\it\mu}_{r}=3.2$
for a two-spike configuration, depicted in (b), that has bifurcated off the flat state. The state in (b) was computed for
![]() $B=11.3~\text{mT}$
. We terminated the branch early.
$B=11.3~\text{mT}$
. We terminated the branch early.
In a second attempt, we select a smaller value of magnetic permeability, namely
![]() ${\it\mu}_{r}=2$
. Here we find that, while the critical value of the induction is far from that experimentally observed, the width of the bistability region between the flat state and the domain-covering hexagons is very close (approximately 0.25 mT in both experiments and numerics); see figure 13. Furthermore, we find from the numerics at the fold of the domain-covering hexagons that the predicted height of the hexagons is 1.2 mm (from figure 4 we find the measured height of 1.3 mm) and at onset the height of the stable hexagons is predicted to be 2.4 mm (and from figure 4 we find the measured height of 2.4 mm), i.e. in the bistability region the numerics are within 5 % error of that experimentally observed. Hence, it is possible that phenomenologically
${\it\mu}_{r}=2$
. Here we find that, while the critical value of the induction is far from that experimentally observed, the width of the bistability region between the flat state and the domain-covering hexagons is very close (approximately 0.25 mT in both experiments and numerics); see figure 13. Furthermore, we find from the numerics at the fold of the domain-covering hexagons that the predicted height of the hexagons is 1.2 mm (from figure 4 we find the measured height of 1.3 mm) and at onset the height of the stable hexagons is predicted to be 2.4 mm (and from figure 4 we find the measured height of 2.4 mm), i.e. in the bistability region the numerics are within 5 % error of that experimentally observed. Hence, it is possible that phenomenologically
![]() ${\it\mu}_{r}=2$
is the appropriate value to take in the linear magnetisation law for the numerics for localised hexagon patches.
${\it\mu}_{r}=2$
is the appropriate value to take in the linear magnetisation law for the numerics for localised hexagon patches.

Figure 13. Maximum height of the domain-covering pattern (black line) computed numerically for
![]() ${\it\mu}_{r}=2$
at the critical wavenumber
${\it\mu}_{r}=2$
at the critical wavenumber
![]() $k_{\mathit{c}}\approx 608.94~\text{m}^{-1}$
versus the magnetic induction. The maximum height of the rhomboid patches is marked by a brown line.
$k_{\mathit{c}}\approx 608.94~\text{m}^{-1}$
versus the magnetic induction. The maximum height of the rhomboid patches is marked by a brown line.
The heights of the spikes in the patches are found numerically to be highest at the core of the patch and decrease as the spikes get closer to the edge of the patch. As shown in figure 13(a), the maximum height of the rhomboid patches is slightly larger than the domain-covering hexagons, similar to that seen in the experiments.
The numerical observation of various coexisting hexagon patches in figure 9, in the bistability region of the flat state and the domain-covering hexagons, agrees well with the experimental results shown in figure 6, where for the same
![]() $B_{3}$
values several different patches were observed. In particular, we are able to find numerically patches (figure 10
a–d) that look to be identical to those seen in figure 5(b,d,f,i). Our numerical methods imposed that the patches should have
$B_{3}$
values several different patches were observed. In particular, we are able to find numerically patches (figure 10
a–d) that look to be identical to those seen in figure 5(b,d,f,i). Our numerical methods imposed that the patches should have
![]() $\mathbb{D}_{2}$
symmetry; hence we were unable to locate any of the other patches seen in figure 5. However, owing to the existence of a Maxwell point nearby, we believe hexagon spikes/cells can be added to the patches to break the
$\mathbb{D}_{2}$
symmetry; hence we were unable to locate any of the other patches seen in figure 5. However, owing to the existence of a Maxwell point nearby, we believe hexagon spikes/cells can be added to the patches to break the
![]() $\mathbb{D}_{2}$
symmetry provided you are in the
$\mathbb{D}_{2}$
symmetry provided you are in the
![]() $\langle 11\rangle$
hexagon front snaking region. Hence, we have a possible explanation for the existence of all the various types of patches observed experimentally.
$\langle 11\rangle$
hexagon front snaking region. Hence, we have a possible explanation for the existence of all the various types of patches observed experimentally.
Perhaps the largest difference between the numerical and experimental results is that the sequence of plateaux for fixed
![]() ${\it\tau}_{2}$
suggests that one can climb up the snakes for increasing
${\it\tau}_{2}$
suggests that one can climb up the snakes for increasing
![]() $B_{3}$
, i.e. the snakes are not vertical as in figures 9 or 10 but slanted, as found by Firth, Columbo & Scroggie (Reference Firth, Columbo and Scroggie2007) and Dawes (Reference Dawes2008) for a conserved quantity. Slanted snaking may emerge in the presence of a nonlinear magnetisation law and finite-domain effects, and could provide an explanation for the emergence of larger and larger patches seen in figure 10.
$B_{3}$
, i.e. the snakes are not vertical as in figures 9 or 10 but slanted, as found by Firth, Columbo & Scroggie (Reference Firth, Columbo and Scroggie2007) and Dawes (Reference Dawes2008) for a conserved quantity. Slanted snaking may emerge in the presence of a nonlinear magnetisation law and finite-domain effects, and could provide an explanation for the emergence of larger and larger patches seen in figure 10.
8. Conclusion and outlook
Utilising a magnetic pulse sequence, we prepare a ferrofluidic layer to be situated next to the unstable branch of the Rosensweig instability. There, localised hexagon patches emerge spontaneously. The measured sequence of patches indicates homoclinic snaking. This is corroborated by numerics, where we investigate the Young–Laplace equation coupled to the Maxwell equations. Homoclinic snaking is demonstrated for two types of planar hexagon fronts as well as hexagon and rhomboid patches. The experimentally observed sequence of patterns can be interpreted as an imperfect mixture of those prototype scenarios. The numerically unveiled Maxwell point of the hexagons provides an energy argument for those various regular and irregular patches observed, since near the Maxwell point the energy of a single hexagon spike is the same as the flat state and there is no energy penalty in adding/removing hexagon spikes. The width of the experimentally observed plateaux is about 0.5 % of the control parameter, which is comparable to the snaking interval of the numerical prototypes. Moreover, the height of the patches in experiment and numerics agrees within 10 %. Therefore, we believe that our model captures all the most important phenomena of the system. In particular, as the relative magnetic permeability tends to unity, the validity of our model increases. It thus unveils an organising centre for the emergence of localised hexagon patches seen in the experiment.

Figure 14. (a) Bifurcation diagram of the domain-covering hexagons for
![]() ${\it\mu}_{r}=2$
on the domain
${\it\mu}_{r}=2$
on the domain
![]() $(x,y)\in [-2{\rm\pi},2{\rm\pi}]\times [-2{\rm\pi}/\sqrt{3},2{\rm\pi}/\sqrt{3}]$
with
$(x,y)\in [-2{\rm\pi},2{\rm\pi}]\times [-2{\rm\pi}/\sqrt{3},2{\rm\pi}/\sqrt{3}]$
with
![]() $N_{x}=N_{y}=20$
,
$N_{x}=N_{y}=20$
,
![]() $D=10$
and varying
$D=10$
and varying
![]() $N_{z}$
. (b) Bifurcation diagram of the domain-covering hexagons for
$N_{z}$
. (b) Bifurcation diagram of the domain-covering hexagons for
![]() ${\it\mu}_{r}=2$
on the domain
${\it\mu}_{r}=2$
on the domain
![]() $(x,y)\in [-2{\rm\pi},2{\rm\pi}]\times [-2{\rm\pi}/\sqrt{3},2{\rm\pi}/\sqrt{3}]$
with
$(x,y)\in [-2{\rm\pi},2{\rm\pi}]\times [-2{\rm\pi}/\sqrt{3},2{\rm\pi}/\sqrt{3}]$
with
![]() $N_{z}=20$
and varying
$N_{z}=20$
and varying
![]() $N_{x}$
(
$N_{x}$
(
![]() $N_{y}=N_{x}$
). (c) Relative error on a semi-log scale of the L2 norm of the interface
$N_{y}=N_{x}$
). (c) Relative error on a semi-log scale of the L2 norm of the interface
![]() $\Vert {\it\zeta}\Vert _{2}^{2}$
for the domain-covering hexagons on the upper branch at
$\Vert {\it\zeta}\Vert _{2}^{2}$
for the domain-covering hexagons on the upper branch at
![]() $({\it\epsilon},{\it\mu}_{r})=(0,2)$
with
$({\it\epsilon},{\it\mu}_{r})=(0,2)$
with
![]() $N_{z}=20,D=10$
and varying
$N_{z}=20,D=10$
and varying
![]() $N_{x}=N_{y}$
with respect to the hexagon computed for
$N_{x}=N_{y}$
with respect to the hexagon computed for
![]() $N_{z}=22,N_{x}=N_{y}=22$
. (d) Relative error on a semi-log scale of the L2 norm of the interface
$N_{z}=22,N_{x}=N_{y}=22$
. (d) Relative error on a semi-log scale of the L2 norm of the interface
![]() $\Vert {\it\zeta}\Vert _{2}^{2}$
for the domain-covering hexagons on the upper branch at
$\Vert {\it\zeta}\Vert _{2}^{2}$
for the domain-covering hexagons on the upper branch at
![]() $({\it\epsilon},{\it\mu}_{r})=(0,2)$
with
$({\it\epsilon},{\it\mu}_{r})=(0,2)$
with
![]() $N_{x}=N_{y}=20,D=10$
and varying
$N_{x}=N_{y}=20,D=10$
and varying
![]() $N_{z}$
with respect to the hexagon computed for
$N_{z}$
with respect to the hexagon computed for
![]() $N_{z}=22,N_{x}=N_{y}=22$
. From both (c) and (d) we observe rapid (geometric) convergence due to the spectral accuracy of the numerical pseudo-spectral methods.
$N_{z}=22,N_{x}=N_{y}=22$
. From both (c) and (d) we observe rapid (geometric) convergence due to the spectral accuracy of the numerical pseudo-spectral methods.
It still remains to explore how various stable configurations of patches connect via unstable branches both experimentally (by quasi-statically varying the magnetic induction
![]() $B$
once a patch has been generated) and theoretically. The discrepancy between the experimental indications for slanted snaking and the vertical snaking obtained numerically may be solved by incorporating a nonlinear magnetisation law, finite-size and shallow-layer effects or by carrying out more experiments to determine the precise extent of the plateaux.
$B$
once a patch has been generated) and theoretically. The discrepancy between the experimental indications for slanted snaking and the vertical snaking obtained numerically may be solved by incorporating a nonlinear magnetisation law, finite-size and shallow-layer effects or by carrying out more experiments to determine the precise extent of the plateaux.

Figure 15. Normal-form results of Silber & Knobloch (Reference Silber and Knobloch1988) showing the changes in sub- and supercriticality of the bifurcations for rolls, squares and up-hexagons, i.e. hexagons whose maximum amplitude is positive.
Theoretically, there are now some very interesting directions one could take. With the existence of an energy functional for the full system that incorporates the boundary conditions, one could look at applying variational and spatial-dynamical techniques that have been developed in the water–wave literature (see e.g. Groves & Sun Reference Groves and Sun2008; Buffoni et al. Reference Buffoni, Groves, Sun and Wahlén2013).
Acknowledgements
The authors confirm that data underlying the findings are available without restriction. Details of the data and how to request access are available from the University of Surrey publications repository: http://epubs.surrey.ac.uk/id/eprint/807861. D.J.B.L. acknowledges support from an EPSRC grant (Nucleation of Ferrosolitons and Ferropatterns) EP/H05040X/1 and many fruitful discussions with M. Groves. Moreover, the authors thank A. Beetz and R. Maretzki for recording the high density range picture in figure 1, and K. Oetter for assistance in constructing the experimental set-up. In memory of R. Friedrich.
Supplementary movie
A supplementary movie is available at http://dx.doi.org/10.1017/jfm.2015.565.
Appendix. Validation of the numerical scheme
We present an overview of the validation results of the numerical scheme. We first plot a convergence test for the domain-covering hexagons for
![]() $({\it\epsilon},{\it\mu}_{r})=(0,2)$
on the domain
$({\it\epsilon},{\it\mu}_{r})=(0,2)$
on the domain
![]() $(x,y)\in [-2{\rm\pi},2{\rm\pi}]\times [-2{\rm\pi}/\sqrt{3},2{\rm\pi}/\sqrt{3}]$
and
$(x,y)\in [-2{\rm\pi},2{\rm\pi}]\times [-2{\rm\pi}/\sqrt{3},2{\rm\pi}/\sqrt{3}]$
and
![]() $D=10$
. In figure 14, we plot the relative error (relative to a hexagon spike computed with
$D=10$
. In figure 14, we plot the relative error (relative to a hexagon spike computed with
![]() $N_{x}=N_{y}=40$
) as
$N_{x}=N_{y}=40$
) as
![]() $N_{x}=N_{y}=N$
is varied and then as
$N_{x}=N_{y}=N$
is varied and then as
![]() $N_{z}$
is varied. Since we are using pseudo-spectral methods, we see rapid (geometric) convergence with few mesh points. For our numerical results, we have a relative error of
$N_{z}$
is varied. Since we are using pseudo-spectral methods, we see rapid (geometric) convergence with few mesh points. For our numerical results, we have a relative error of
![]() $10^{-3}$
and the fold points are computed to a relative error of
$10^{-3}$
and the fold points are computed to a relative error of
![]() $10^{-4}$
.
$10^{-4}$
.
In order to test that we have correctly captured the nonlinearity in the system, we compare our results with the normal-form analysis of Silber & Knobloch (Reference Silber and Knobloch1988) shown in figure 15. Since the analysis is for small amplitude, we only compare the bifurcation transitions for each of the rolls and squares from sub- to supercritical. Here we find excellent agreement with our numerics, giving us confidence in our results, as shown in figure 16, where we plot the existence regions of the rolls, squares and hexagons for
![]() ${\it\epsilon}<0$
. The final validation we carried out was to find that the Maxwell point computed for
${\it\epsilon}<0$
. The final validation we carried out was to find that the Maxwell point computed for
![]() ${\it\mu}_{r}=1.9$
lies in the middle of the snaking region of both the
${\it\mu}_{r}=1.9$
lies in the middle of the snaking region of both the
![]() $\langle 10\rangle$
and
$\langle 10\rangle$
and
![]() $\langle 11\rangle$
fronts in figure 8 as predicted by Woods & Champneys (Reference Woods and Champneys1999) and Coullet et al. (Reference Coullet, Riera and Tresser2000). This demonstrates that the discretisation of (5.3b,c
) and (5.4a
) is consistent with the energy/Hamiltonian formalisation (5.7) and (5.10) and we are solving the correct equations.
$\langle 11\rangle$
fronts in figure 8 as predicted by Woods & Champneys (Reference Woods and Champneys1999) and Coullet et al. (Reference Coullet, Riera and Tresser2000). This demonstrates that the discretisation of (5.3b,c
) and (5.4a
) is consistent with the energy/Hamiltonian formalisation (5.7) and (5.10) and we are solving the correct equations.

Figure 16. Numerical computation of existence regions of domain-covering rolls, squares and hexagons for
![]() ${\it\epsilon}<0$
. We observe that all three of the domain-covering patterns bifurcate subcritically in the regions where the normal form theory of Silber & Knobloch (Reference Silber and Knobloch1988) predicts.
${\it\epsilon}<0$
. We observe that all three of the domain-covering patterns bifurcate subcritically in the regions where the normal form theory of Silber & Knobloch (Reference Silber and Knobloch1988) predicts.






















