Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-19T07:33:49.588Z Has data issue: false hasContentIssue false
  • English
  • Français

MOCK THETA FUNCTIONS AND QUANTUM MODULAR FORMS

Part of: Discontinuous groups and automorphic forms Basic hypergeometric functions

Published online by Cambridge University Press:  19 September 2013

AMANDA FOLSOM ,
KEN ONO  and
ROBERT C. RHOADES
AMANDA FOLSOM
Affiliation:
Department of Mathematics, Yale University, New Haven, CT 06520, USAamanda.folsom@yale.edu
KEN ONO
Affiliation:
Department of Mathematics, Emory University, Atlanta, GA 30322, USAono@mathcs.emory.edu
ROBERT C. RHOADES
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, USArhoades@math.stanford.edurob.rhoades@gmail.com

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

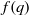Ramanujan’s last letter to Hardy concerns the asymptotic properties of modular forms and his ‘mock theta functions’. For the mock theta function $f(q)$, Ramanujan claims that as 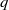$q$ approaches an even-order 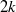$2k$ root of unity, we have

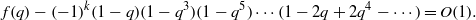$$\begin{eqnarray*}f(q)- (- 1)^{k} (1- q)(1- {q}^{3} )(1- {q}^{5} )\cdots (1- 2q+ 2{q}^{4} - \cdots )= O(1).\end{eqnarray*}$$
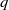We prove Ramanujan’s claim as a special case of a more general result. The implied constants in Ramanujan’s claim are not mysterious. They arise in Zagier’s theory of ‘quantum modular forms’. We provide explicit closed expressions for these ‘radial limits’ as values of a ‘quantum’ $q$-hypergeometric function which underlies a new relationship between Dyson’s rank mock theta function and the Andrews–Garvan crank modular form. Along these lines, we show that the Rogers–Fine false 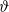$\vartheta $-functions, functions which have not been well understood within the theory of modular forms, specialize to quantum modular forms.

MSC classification

Secondary: 11F99: None of the above, but in this section 11F37: Forms of half-integer weight; nonholomorphic modular forms 33D15: Basic hypergeometric functions in one variable, $_rphi_s$
Type
Research Article
Information
Forum of Mathematics, Pi , Volume 1 , 2013 , e2
Creative Commons
Creative Common License - CCCreative Common License - BY
The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
Copyright
© The Author(s) 2013.

References

Andrews, G. E., ‘On the theorems of Watson and Dragonette for Ramanujan’s mock theta functions’, Amer. J. Math. 88 (1966), 454–490.Google Scholar
Andrews, G. E., ‘Concave and convex compositions’, Ramanujan J., to appear.Google Scholar
Andrews, G. E. and Berndt, B. C., ‘Your hit parade – the top ten most fascinating formulas from Ramanujan’s lost notebook’, Notices Amer. Math. Soc. 55 (2008), 18–30.Google Scholar
Andrews, G. E. and Berndt, B. C., Ramanujan’s Lost Notebook. Part II (Springer, New York, 2009).Google Scholar
Andrews, G. E. and Garvan, F., ‘Dyson’s crank of a partition’, Bull. Amer. Math. Soc. (N.S.) 18 (1988), 167–171.Google Scholar
Andrews, G. E., Ono, K. and Urroz, J., ‘q-identities and values of certain L-functions’, Duke Math. J. 108 (2001), 395–419.CrossRefGoogle Scholar
Andrews, G. E., Rhoades, R. C. and Zwegers, S., ‘Modularity of the concave composition generating function’, Algebra Number Theory, (2013), accepted for publication.Google Scholar
Atkin, A. O. L. and Swinnerton-Dyer, H. P. F., ‘Some properties of partitions’, Proc. Lond. Math. Soc. 4 (1954), 84–106.Google Scholar
Bajpai, J., Kimport, S., Liang, J., Ma, D. and Ricci, J., ‘Bilateral series and Ramanujan’s radial limits’, Proc. Amer. Math. Soc., (2013), accepted for publication.CrossRefGoogle Scholar
Berndt, B. C., ‘Ramanujan, his lost notebook, its importance’, preprint.Google Scholar
Berndt, B. C. and Rankin, R. A., Ramanujan: Letters and Commentary (American Mathematical Society, Providence, 1995).CrossRefGoogle Scholar
Bringmann, K. and Folsom, A., ‘On the asymptotic behavior of Kac–Wakimoto characters’, Proc. Amer. Math. Soc. 141(5) (2013), 1567–1576.Google Scholar
Bringmann, K., Folsom, A. and Rhoades, R. C., ‘Partial and mock theta functions as $q$-hypergeometric series’, in Ramanujan’s 125th Anniversary Special Volume, Ramanujan J. 29(1–3) (2012), 295–310 (special issue).Google Scholar
Bringmann, K., Mahlburg, K. and Rhoades, R. C., ‘Taylor coefficients of mock-Jacobi forms and moments of partition statistics’, Math. Proc. Cambridge Philos. Soc., to appear.Google Scholar
Bringmann, K. and Ono, K., ‘The $f(q)$ mock theta function conjecture and partition ranks’, Invent. Math. 165 (2006), 243–266.Google Scholar
Bringmann, K. and Ono, K., ‘Dyson’s ranks and Maass forms’, Ann. of Math. 171 (2010), 419–449.Google Scholar
Bringmann, K., Ono, K. and Rhoades, R., ‘Eulerian series as modular forms’, J. Amer. Math. Soc. 21 (2008), 1085–1104.Google Scholar
Bruinier, J. H. and Funke, J., ‘On two geometric theta lifts’, Duke Math. J. 125 (2004), 45–90.Google Scholar
Bryson, J., Ono, K., Pitman, S. and Rhoades, R. C., ‘Unimodal sequences and quantum and mock modular forms’, Proc. Natl. Acad. Sci. USA 109(40) (2012), 16063–16067.CrossRefGoogle Scholar
Choi, Y.-S., ‘The basic bilateral hypergeometric series and the mock theta functions’, Ramanujan J. 24 (2011), 345–386.CrossRefGoogle Scholar
Coogan, G. and Ono, K., ‘A $q$-series identity and the arithmetic of Hurwitz-zeta functions’, Proc. Amer. Math. Soc. 131 (2003), 719–724.Google Scholar
Dragonette, L., ‘Some asymptotic formulae for the mock theta series of Ramanujan’, Trans. Amer. Math. Soc. 72 (1952), 474–500.Google Scholar
Dyson, F., ‘Some guesses in the theory of partitions’, Eureka 8 (1944), 10–15.Google Scholar
Fine, N. J., Basic Hypergeometric Series and Applications, Math. Surveys and Monographs, 27 (American Mathematical Society, Providence, 1988).Google Scholar
Folsom, A., ‘Mock modular forms and $d$-distinct partitions’, preprint.Google Scholar
Gasper, G. and Rahman, M., Basic Hypergeometric Series, Ency. Math. and App., 35 (Cambridge University Press, Cambridge, 1990).Google Scholar
Gordon, B. and McIntosh, R., ‘A survey of classical mock theta functions’, in Partitions, q-series and Mmodular Forms, Dev. Math., 23 (Springer, New York, 2012), 95–144.CrossRefGoogle Scholar
Griffin, M., Ono, K. and Rolen, L., ‘Ramanujan’s mock theta functions’, Proc. Natl. Acad. Sci., USA 110 (2013), 5765–5768.CrossRefGoogle ScholarPubMed
Hikami, K., ‘Quantum invariant for torus link and modular forms’, Comm. Math. Phys. 246 (2004), 403–426.Google Scholar
Kubert, D. S. and Lang, S., Modular Units (Springer, Berlin, 1981).Google Scholar
Lawrence, R. and Zagier, D., ‘Modular forms and quantum invariants of 3-manifolds’, Asian J. Math. 3 (1999), 93–108.Google Scholar
Lovejoy, J. and Ono, K., ‘Hypergeometric generating functions for the values of Dirichlet and other $L$-functions’, Proc. Natl. Acad. Sci., USA 100 (2003), 6904–6909.Google Scholar
Mahlburg, K., ‘Partition congruences and the Andrews–Garvan–Dyson crank’, Proc. Natl. Acad. Sci. USA 105 (2005), 15373–15376.CrossRefGoogle Scholar
Mortenson, E. T., ‘On the dual nature of partial theta functions and Appell–Lerch sums’, preprint. arxiv:1208.6316.Google Scholar
Ono, K., ‘Unearthing the visions of a master: harmonic Maass forms and number theory’, Proc. 2008 Harvard-MIT Current Developments in Mathematics Conf., (2009), Somerville, Ma., 347–454.Google Scholar
Rademacher, H., Topics in Analytic Number Theory, Die Grund. der math. Wiss., Band, 169 (Springer, New York–Heidelberg, 1973).Google Scholar
Rhoades, R. C., ‘Asymptotics for the number of strongly unimodal sequences’, Int. Math. Res. Not., to appear.Google Scholar
Rhoades, R. C., ‘A unified approach to partial and mock theta functions’, Math. Res. Lett., to appear.Google Scholar
Rogers, L., ‘On two theorems of combinatory analysis and some allied identities’, Proc. Lond. Math. Soc. (2) 16 (1917), 315–336.Google Scholar
Watson, G. N., ‘The final problem: an account of the mock theta functions’, J. Lond. Math. Soc. 2(2) (1936), 55–80.Google Scholar
Zagier, D., ‘Vassiliev invariants and a strange identity related to the Dedekind eta-function’, Topology 40 (2001), 945–960.Google Scholar
Zagier, D., ‘Ramanujan’s mock theta functions and their applications [d’aprés Zwegers and Bringmann–Ono]’, Sém. Bourbaki (2007/2008), Astérisque, No. 326, Exp. No. 986, vii–viii, (2010), 143–164.Google Scholar
Zagier, D., ‘Quantum modular forms’, in Quanta of Maths: Conference in Honor of Alain Connes, Clay Mathematics Proceedings, 11 (American Mathematical Society, Providence, 2010), 659–675.Google Scholar
Zwegers, S., ‘Mock $\vartheta $-functions and real analytic modular forms’, in q-series with Applications to Combinatorics, Number Theory, and Physics, Contemporary Mathematics, 291 (eds. Berndt, B. C. and Ono, K.) (American Mathematical Society, 2001), 269–277.Google Scholar
Zwegers, S., Mock Theta Functions, Ph.D. Thesis (Advisor: D. Zagier), (Universiteit Utrecht, 2002).Google Scholar
Zwegers, S., ‘Multivariable Appell functions’, preprint.Google Scholar