Hostname: page-component-8448b6f56d-qsmjn Total loading time: 0 Render date: 2024-04-19T18:49:34.828Z Has data issue: false hasContentIssue false
  • English
  • Français

On the initial growth of interfaces in reaction–diffusion equations with strong absorption

Published online by Cambridge University Press:  14 November 2011

Luis Alvarez  and
Jesus Ildefonso Diaz
Luis Alvarez
Affiliation:
Depto. de Informatica y Sistemas, Univ. de Las Palmas, 35017, Las Palmas, Spain
Jesus Ildefonso Diaz
Affiliation:
Depto. de Matematica Aplicada, Univ. Complutense de Madrid, 28040 Madrid, Spain
Get access Rights & Permissions [Opens in a new window]

Extract

We study the initial growth of the interfaces of non-negative local solutions of the equation ut = (um)xx−λuq when m ≧ 1 and 0<q <1. We show that if 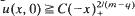with C < C0, for some explicit C0 = C0(λ, m, q), then the free boundary Ϛ(t) = sup {x:u(x, t) > 0} is a ‘heating front’. More precisely Ϛ(t) ≧at(m−q)/2(1−q) for any t small enough and for some a>0. If on the contrary, 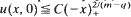with C<C0, then Ϛ(t) is a ‘cooling front’ and in fact Ϛ(t) ≧ −atm−q)/2(1−q) for any t small enough and for some a > 0. Applications to solutions of the associated Cauchy and Dirichlet problems are also given.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 5 , 1993 , pp. 803 - 817
Copyright
Copyright © Royal Society of Edinburgh 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Alvarez, L.. On the behavior of the free boundary of some nonhomogeneous elliptic problems. Applicable Anal. 36 (1990), 131–144.CrossRefGoogle Scholar
2Alvarez, L. and Díaz, J. I.. On the behavior near the free boundary of solutions of some nonhomogeneous elliptic problems. In Adas IX C.E.D.Y.A. (Ed. Univ. de Valladolid, 1986), pp. 55–59.Google Scholar
3Alvarez, L. and Díaz, J. I.. Sufficient and necessary initial mass conditions for the existence of a waiting time in nonlinear-convection processes. J. Math. Anal. Appl. 155 (1991), 378–392.CrossRefGoogle Scholar
4Alvarez, L., Díaz, J. I. and Kersner, R.. On the initial growth of the interfaces in nonlinear diffusion-convection processes. In Nonlinear Diffusion Equations and Their Equilibrium States, eds Ni, W.-M., Peletier, L. A. and Serrin, J., pp. 1–20 (Berlin: Springer, 1988).Google Scholar
5Antontsev, S. N. and Díaz, J. I.. New results on localization of solutions of nonlinear elliptic and parabolic equations obtained by the energy methods. Dokl. Acad. Nauk 303 (1988), 524–529 (in Russian); English translation: Soviet. Mat. Dokl. 38 (1988), 535–539.Google Scholar
6Bandle, C. and Stakgold, I.. The formation of the dead core in parabolic reaction-diffusion problems. Trans. Amer. Math. Soc. 286 (1984), 275–293.CrossRefGoogle Scholar
7Benilan, Ph., Crandall, M. G. and Pierre, M.. Solutions of the porous medium equation in RN under optimal conditions on initial value. Indiana Univ. Math. J. 33 (1984), 51–87.CrossRefGoogle Scholar
8Bernis, F.. Finite speed of propagation and asymptotic rates for some nonlinear higher order parabolic equations with absorption. Proc. Roy. Soc. Edinburgh Sect. A 104 (1986), 1–19.CrossRefGoogle Scholar
9Bertsch, M.. A class of degenerate diffusion equations with a singular nonlinear term. Nonlinear Anal. 7(1983), 117–127.CrossRefGoogle Scholar
10Crank, J. and Gupta, R. S.. A moving boundary problem arising from the diffusion of oxygen in absorbing tissue. J. Inst. Math. Appl. 10 (1972), 19–33.CrossRefGoogle Scholar
11Díaz, G.. On the positivity set of solutions of semilinear equations by stochastic methods. In Free Boundary Problems: Theory and Applications, Vol. II, eds Haffman, K. H. and Sprekels, J. pp. 833–840 (Harlow: Longman, 1990).Google Scholar
12Díaz, J. I.. Nonlinear Partial Differential Equations and Free Boundaries: Vol. 1 Elliptic Equations, Research Notes in Mathematics 106 (London: Pitman, 1985).Google Scholar
13Díaz, J. I. and Hernandez, J.. Some results on the existence of free boundaries for parabolic reaction-diffusion systems. In Trends in Theory and Practice of Nonlinear Differential Equations, ed. Lakshmikanthan, V., Proceeding of a meeting held at Lexington, Texas, June, 1982, pp. 149–156 (New York: Marcel Dekker, 1984).Google Scholar
14Díaz, J. I. and Hernandez, J.. Qualitative properties of free boundaries for some nonlinear degenerate parabolic equations. In Nonlinear parabolic equations: qualitative properties of solutions, pp. 85–93 (Harlow: Longman, 1987).Google Scholar
15Friedman, A.. Partial Differential Equations of the Parabolic Type (Englewood Cliffs N.J.: Prentice-Hall, 1969).Google Scholar
16Friedman, A. and Herrero, M. A.. Extinction properties of semilinear heat equations with strong absorption. J. Math. Anal. Appl. 124 (1987), 530–546.CrossRefGoogle Scholar
17Grundy, R. E.. Asymptotic solutions of a model diffusion-reaction equation. IMA J. Appl. Math. 40 (1988), 53–72.CrossRefGoogle Scholar
18Grundy, R. E. and Peletier, L. A.. Short time behavior of a singular solution to the heat equation with absorption. Proc. Roy. Soc. Edinburgh Sect A 107 (1987), 271–288.CrossRefGoogle Scholar
19Grundy, R. E. and Peletier, L. A.. The initial interface development for a reaction-diffusion equation with power law initial data. Quart. J. Mech. Appl. Math, (to appear).Google Scholar
20Gutman, S. and Martin, R. H. JrThe porous medium equation with nonlinear absorption and moving boundaries. Israel J. Math. 54 (1986), 81–109.CrossRefGoogle Scholar
21Herrero, M. A. and Vazquez, J. L.. The one-dimensional nonlinear heat equation with absorption: Regularity of solutions and interfaces. SIAM J. Math. Anal. 18 (1987), 149–167.CrossRefGoogle Scholar
22Herrero, M. A. and Vazquez, J. L.. Thermal waves in absorbing media. J. Differential Equations 74 (1988), 218–233.CrossRefGoogle Scholar
23Herrero, M. A. and Velazquez, J. J. L.. On the dynamics of a semilinear heat equation with strong absorption. Comm. Partial Differential Equations 14 (1989), 1653–1715.CrossRefGoogle Scholar
24Kalashnikov, A. S.. The propagation of disturbances in problems of non-linear heat conduction with absorption. USSR. Comput. Math, and Math. Phys. 14 (1974), 70–85.CrossRefGoogle Scholar
25Kalashnikov, A. S.. The effect of absorption on heat propagation in a medium in which the thermal conductivity depends on temperature. U.S.S.R. Comput. Math, and Math. Phys. 16 (1976), 141–149.CrossRefGoogle Scholar
26Kamin, S., Peletier, L. A. and Vazquez, J. L.. A nonlinear diffusion-absorption equation with unbounded data. In Nonlinear diffusion equations and their equilibrium states. III, eds Lloyd, N. G.et al., pp. 243–263 (Boston: Birkhauser, 1992).CrossRefGoogle Scholar
27Kersner, R.. The behavior of temperature fronts in media with nonlinear thermal conductivity under absorption. Moscow Univ. Math. Bull. 31 (1976), 90–95.Google Scholar
28Kersner, R..Degenerate parabolic equations with general nonlinearities. Nonlinear Anal. 4 (1984), 1043–1062.CrossRefGoogle Scholar
29Knerr, B. F.. The behavior of the support of solutions of the equation of nonlinear heat conduction with absorption in one dimension. Trans. Amer. Math. Soc. 249 (1979), 409–424.CrossRefGoogle Scholar
30Langlais, M. and Phillips, D.. Stabilization of solutions of nonlinear and degenerate evolution problems. Nonlinear Anal. 9 (1985), 321–333.CrossRefGoogle Scholar
31Palymskii, I. B.. Some qualitative properties of solutions of nonlinear heat equations for nonlinear heat conductivity with absorption. In Chislenye Met. Mekh. Sploshnoi Sredy (Novosibirsk) 16 (1985), 136–145.Google Scholar
32Rosenau, P. and Kamin, S.. Thermal waves in an absorbing and convecting medium. Phys. D 8 (1983), 273–283.CrossRefGoogle Scholar
33Vazquez, J. L.. The interfaces of one-dimensional flows in porous media. Trans. Amer. Math. Soc. 285 (1984), 717–737.CrossRefGoogle Scholar