Hostname: page-component-8448b6f56d-c47g7 Total loading time: 0 Render date: 2024-04-19T06:59:17.326Z Has data issue: false hasContentIssue false
  • English
  • Français

Counterexamples to the modified Weyl–Berry conjecture on fractal drums

Published online by Cambridge University Press:  24 October 2008

Michel L. Lapidus  and
Carl Pomerance
Michel L. Lapidus
Affiliation:
Department of Mathematics, Sproul Hall, University of California, Riverside, CA 92521-0135, U.S.A, e-mail: lapidus@math.ucr.edu
Carl Pomerance
Affiliation:
Department of Mathematics, University of Georgia, Boyd Graduate Studies Research Center, Athens, GA 30602, U.S.A, e-mail: carl@ada.math.uga.edu
Get access Rights & Permissions [Opens in a new window]

Extract

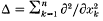Let Ω be a non-empty open set in ℝn with finite ‘volume’ (n-dimensional Lebesgue measure). Let be the Laplacian operator. Consider the eigenvalue problem (with Dirichlet boundary conditions):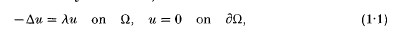

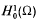where λ ∈ ℝ and u is a non-zero member of (the closure in the Sobolev space H1(Ω) of the set of smooth functions with compact support contained in Ω). It is well known that the values of λ∈ℝ for which (1·1) has a non-zero solution 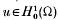are positive and form a discrete set. Moreover, for each λ, the associated eigenspace is finite dimensional. Let the spectrum of (1·1) be denoted 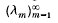where 0 < λ1 ≤ λ2 ≤ … and where the multiplicity of each λ in the sequence is the dimension of the associated eigenspace. Let

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 119 , Issue 1 , January 1996 , pp. 167 - 178
Copyright
Copyright © Cambridge Philosophical Society 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Birman, M. S. and Solomjak, M. Z.. The principal term of the spectral asymptotics for nonsmooth elliptic problems. Funktsional. Anal. i Prilhozen 4, no. 4 (1970), 1–13.Google Scholar
[2]Brossard, J. and Carmona, R.. Can one hear the dimension of a fractal? Comm. Math. Phys. 104 (1986). 103–122.CrossRefGoogle Scholar
[3]Doob, J. L.. Classical potential theory and its probabilistic counterpart (Springer-Verlag, 1984).CrossRefGoogle Scholar
[4]Falconer, K.. On the Minkowski measurability of fractals. Proc. Amer. Math. Soc., to appear.Google Scholar
[5]Fleckinger-Pellé, J. and Vassiliev, D. G.. An example of a two-term asymptotics for the ‘counting function’ of a fractal drum. Trans. Amer. Math. Soc. 337 (1993), 99116.Google Scholar
[6]Hörmander, L.. The analysis of linear partial differential operators, vols, III, IV (Springer-Verlag, 1985).Google Scholar
[7]Kuznetsov, N. V.. Asymptotic distribution of the eigenfrequencies of a plane membrane in the case when the variables can be separated. Differential Equations 2 (1966), 715–723.Google Scholar
[8]Lapidus, M. L.. Fractal drum, inverse spectral problems for elliptic operators and a partial resolution of the Weyl-Berry conjecture. Trans. Amer. Math. Soc. 325 (1991), 465–529.CrossRefGoogle Scholar
[9]Lapidus, M. L.. Spectral and fractal geometry: from the Weyl-Berry conjecture for the vibrations of fractal drums to the Riemann zeta-function; in Differential Equations and Mathematical Physics. Proc. Fourth UAB Intern. Conf., Birmingham, Alabama, March 1990 (ed. Bennewitz, C., Academic Press, 1992), pp. 151–182.Google Scholar
[10]Lapidus, M. L.. Vibrations of fractal drums, the Riemann hypothesis, waves in fractal media, and the Weyl-Berry conjecture; in Ordinary and partial differential equations, vol. IV, Proc. Twelfth Dundee Intern. Conf., Dundee, Scotland, UK, June 1992 (eds. Sleeman, B. D. and Jarvis, R. J.), Pitman Research Notes in Math. Series 289 (Longman Scientific and Technical, 1993), pp. 126–209.Google Scholar
[11]Lapidus, M. L. and Fleckinger-Pellé, J.. Tambour fractal: vers une résolution de la conjecture de Weyl-Berry pour les valeurs propres du laplacien. C.R. Acad. Sci. Paris Sér. I Math. 306 (1988), 171–175.Google Scholar
[12]Lapidus, M. L. and Pomerance, C.. Fonction zêta de Riemann et conjecture de Weyl-Berry pour les tambours fractals. C.R. Acad. Sci. Paris Sér. I Math. 310, No. 6 (1990), 343–348.Google Scholar
[13]Lapidus, M. L. and Pomerance, C.. The Riemann zeta-function and the one-dimensional Weyl-Berry conjecture for fractal drums. Proc. London Math. Soc. (3) 66, No. 1 (1993), 41–69.CrossRefGoogle Scholar
[14]Lapidus, M. L. and Pomerance, C.. Abstract no. 865–11–73 (865th Meeting of the Amer. Math. Soc., Tampa, March 1991), Abstracts Amer. Math. Soc. 12, No. 2 (1991), p. 238.Google Scholar
[15]Rauch, J. and Taylor, M.. Potential and scattering theory on wildly perturbed domains. J. Funct. Anal. 18 (1975), 25–59.CrossRefGoogle Scholar