Article contents
Invariants for slightly heated decaying grid turbulence
Published online by Cambridge University Press: 26 June 2013
Abstract
The paper examines the validity of velocity and scalar invariants in slightly heated and approximately isotropic turbulence generated by passive conventional grids. By assuming that the variances 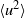 $\langle {u}^{2} \rangle $ and
$\langle {u}^{2} \rangle $ and 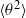 $\langle {\theta }^{2} \rangle $ (
$\langle {\theta }^{2} \rangle $ ( $u$ and
$u$ and 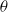 $\theta $ represent the longitudinal velocity and temperature fluctuations) decay along the streamwise direction
$\theta $ represent the longitudinal velocity and temperature fluctuations) decay along the streamwise direction  $x$ according to power laws
$x$ according to power laws 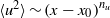 $\langle {u}^{2} \rangle \sim {(x- {x}_{0} )}^{{n}_{u} } $ and
$\langle {u}^{2} \rangle \sim {(x- {x}_{0} )}^{{n}_{u} } $ and 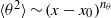 $\langle {\theta }^{2} \rangle \sim {(x- {x}_{0} )}^{{n}_{\theta } } $ (
$\langle {\theta }^{2} \rangle \sim {(x- {x}_{0} )}^{{n}_{\theta } } $ (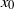 ${x}_{0} $ is the virtual origin of the flow) and with the further assumption that the one-point energy and scalar variance budgets are represented closely by a balance between the rates of change of
${x}_{0} $ is the virtual origin of the flow) and with the further assumption that the one-point energy and scalar variance budgets are represented closely by a balance between the rates of change of 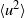 $\langle {u}^{2} \rangle $ and
$\langle {u}^{2} \rangle $ and 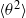 $\langle {\theta }^{2} \rangle $ and the corresponding mean energy dissipation rates, the products
$\langle {\theta }^{2} \rangle $ and the corresponding mean energy dissipation rates, the products 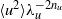 $\langle {u}^{2} \rangle { \lambda }_{u}^{- 2{n}_{u} } $ and
$\langle {u}^{2} \rangle { \lambda }_{u}^{- 2{n}_{u} } $ and 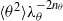 $\langle {\theta }^{2} \rangle { \lambda }_{\theta }^{- 2{n}_{\theta } } $ must remain constant with respect to
$\langle {\theta }^{2} \rangle { \lambda }_{\theta }^{- 2{n}_{\theta } } $ must remain constant with respect to  $x$. Here
$x$. Here 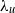 ${\lambda }_{u} $ and
${\lambda }_{u} $ and 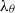 ${\lambda }_{\theta } $ are the Taylor and Corrsin microscales. This is unambiguously supported by previously available data, as well as new measurements of
${\lambda }_{\theta } $ are the Taylor and Corrsin microscales. This is unambiguously supported by previously available data, as well as new measurements of  $u$ and
$u$ and 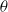 $\theta $ made at small Reynolds numbers downstream of three different biplane grids. Implications for invariants based on measured integral length scales of
$\theta $ made at small Reynolds numbers downstream of three different biplane grids. Implications for invariants based on measured integral length scales of  $u$ and
$u$ and 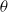 $\theta $ are also tested after confirming that the dimensionless energy and scalar variance dissipation rate parameters are approximately constant with
$\theta $ are also tested after confirming that the dimensionless energy and scalar variance dissipation rate parameters are approximately constant with  $x$. Since the magnitudes of
$x$. Since the magnitudes of 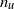 ${n}_{u} $ and
${n}_{u} $ and 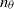 ${n}_{\theta } $ vary from grid to grid and may also depend on the Reynolds number, the Saffman and Corrsin invariants which correspond to a value of
${n}_{\theta } $ vary from grid to grid and may also depend on the Reynolds number, the Saffman and Corrsin invariants which correspond to a value of 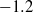 $- 1. 2$ for
$- 1. 2$ for 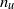 ${n}_{u} $ and
${n}_{u} $ and 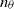 ${n}_{\theta } $ are unlikely to apply in general. The effect of the Reynolds number on
${n}_{\theta } $ are unlikely to apply in general. The effect of the Reynolds number on 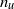 ${n}_{u} $ is discussed in the context of published data for both passive and active grids.
${n}_{u} $ is discussed in the context of published data for both passive and active grids.
- Type
- Papers
- Information
- Copyright
- ©2013 Cambridge University Press
References
- 15
- Cited by




