Hostname: page-component-76fb5796d-qxdb6 Total loading time: 0 Render date: 2024-04-27T08:50:33.354Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniqueness of Morava K-theory

Part of: Categories with structure Operations and obstructions Homology and cohomology theories

Published online by Cambridge University Press:  27 September 2010

Vigleik Angeltveit
Vigleik Angeltveit*
Affiliation:
Department of Mathematics, University of Chicago, Chicago, IL 60637, USA (email: vigleik@math.uchicago.edu)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We show that there is an essentially unique S-algebra structure on the Morava K-theory spectrum K(n), while K(n) has uncountably many MU or 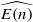-algebra structures. Here 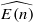is the K(n)-localized Johnson–Wilson spectrum. To prove this we set up a spectral sequence computing the homotopy groups of the moduli space of A∞ structures on a spectrum, and use the theory of S-algebra k-invariants for connectiveS-algebras found in the work of Dugger and Shipley [Postnikov extensions of ring spectra, Algebr. Geom. Topol. 6 (2006), 1785–1829 (electronic)] to show that all the uniqueness obstructions are hit by differentials.

Keywords

S-algebraMorava K-theorymoduli space

MSC classification

Secondary: 55N22: Bordism and cobordism theories, formal group laws 55S35: Obstruction theory 18D50: Operads
Type
Research Article
Information
Compositio Mathematica , Volume 147 , Issue 2 , March 2011 , pp. 633 - 648
Copyright
Copyright © Foundation Compositio Mathematica 2010

References

[1]Angeltveit, V., Topological Hochschild homology and cohomology of A ∞ ring spectra, Geom. Topol. 12 (2008), 987–1032 (electronic).CrossRefGoogle Scholar
[2]Angeltveit, V., Hill, M. and Lawson, T., Topological Hochschild homology of ℓ and ko, Amer. J. Math. 132 (2010), 297–330.CrossRefGoogle Scholar
[3]Boardman, J. M. and Vogt, R. M., Homotopy invariant algebraic structures on topological spaces, Lecture Notes in Mathematics, vol. 347 (Springer, Berlin, 1973).CrossRefGoogle Scholar
[4]Bökstedt, M., The topological hochschild homology of ℤ and ℤ/p. Unpublished.Google Scholar
[5]Bousfield, A. K., Homotopy spectral sequences and obstructions, Israel J. Math. 66 (1989), 54–104.CrossRefGoogle Scholar
[6]Bousfield, A. K. and Kan, D. M., Homotopy limits, completions and localizations, Lecture Notes in Mathematics, vol. 304 (Springer, Berlin, 1972).CrossRefGoogle Scholar
[7]Dugger, D. and Shipley, B., Postnikov extensions of ring spectra, Algebr. Geom. Topol. 6 (2006), 1785–1829 (electronic).CrossRefGoogle Scholar
[8]Dwyer, W. G. and Kan, D. M., A classification theorem for diagrams of simplicial sets, Topology 23 (1984), 139–155.CrossRefGoogle Scholar
[9]Elmendorf, A. D., Kriz, I., Mandell, M. A. and May, J. P., Rings, modules, and algebras in stable homotopy theory (American Mathematical Society, Providence, RI, 1997), with an appendix by M. Cole.Google Scholar
[10]Goerss, P. G. and Hopkins, M. J., Moduli spaces of commutative ring spectra, in Structured ring spectra, London Mathematical Society Lecture Note Series, vol. 315 (Cambridge University Press, Cambridge, 2004), 151–200.CrossRefGoogle Scholar
[11]Lurie, J., Higher topos theory, Annals of Mathematics Studies, vol. 170 (Princeton University Press, Princeton, NJ, 2009).CrossRefGoogle Scholar
[12]Nassau, C., On the structure of P(n)*P((n)) for p=2, Trans. Amer. Math. Soc. 354 (2002), 1749–1757 (electronic).CrossRefGoogle Scholar
[13]Quillen, D., Higher algebraic K-theory. I, in Algebraic K-theory, I: higher K-theories (Proc. Conf., Battelle Memorial Institute, Seattle, WA, 1972), Lecture Notes in Mathematics, vol. 341 (Springer, Berlin, 1973), 85–147.Google Scholar
[14]Ravenel, D. C., Complex cobordism and stable homotopy groups of spheres, second edition (AMS Chelsea Publishing, Providence, RI, 2004).Google Scholar
[15]Rezk, C., Notes on the Hopkins–Miller theorem, in Homotopy theory via algebraic geometry and group representations (Evanston, IL, 1997), Contemporary Mathematics, vol. 220 (American Mathematical Society, Providence, RI, 1998), 313–366.CrossRefGoogle Scholar
[16]Robinson, A., Obstruction theory and the strict associativity of Morava K-theories, in Advances in homotopy theory (Cortona, 1988), London Mathematical Society Lecture Note Series, vol. 139 (Cambridge University Press, Cambridge, 1989), 143–152.CrossRefGoogle Scholar
[17]Robinson, A. and Whitehouse, S., Operads and Γ-homology of commutative rings, Math. Proc. Cambridge Philos. Soc. 132 (2002), 197–234.CrossRefGoogle Scholar